
La tension de surface d'un liquide


Forces intermoléculaires
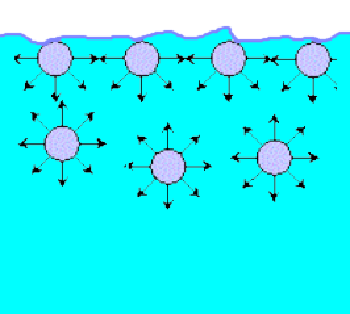
Dans un liquide les molécules s'attirent mutuellement Les molécules en surface sont plutôt attirées vers le corps du liquide (en bas) ou la limite de la surface (tanhentiellement) Toute molécule qui veut prendre leur place ou se mettre à côté pout agrandir la surface doit effectuer un travail contre ces forces et augmentera aisn peu à peu son énergie.

Comparaison: Les alpinistes en B et C doivent fournir un travail pour arriver en A Ceux en A ont emmagasiné la plus grande énergie Les transformations spontanées se feront rnsuite (en ski ?) de haut en bas, de la haute énergie vers une plus bass.
Définition de la tension de surface ($\sigma$)
Tension de surface: $\sigma= \frac{Travail à fournir}{Surface à agrandir} $ $\sigma= \frac{W}{\Delta S}$ Unités : $\frac{J}{m^2}$ Travail à fournir: $W$ = Tenion de surface $\cdot$ Surface à agrandir $W = \sigma \cdot \Delta S$
La surface a ainsi emmagasiné ce travail, la tension de surface est une énergie que possède la surface!
Exemple: Loi de Laplace

La différence de pression entre intérieur $P_i$ et extérieur $P_e$ d'une bulle pleine de liquide de rayon $r$ vaut: $P_i - P_e = \frac{2\sigma}{r}$
Travail à fournir pour augmenter le rayon d'une valeur $dr$: $W = P_i\cdot 4\pi \cdot r^2\cdot dr$ - $P_e\cdot 4\pi \cdot r^2\cdot d$r $\sigma\cdot \Delta S = \Delta P \cdot 4\pi \cdot r^2\cdot dr$ or: ; $\Delta S = 4\pi (r+dr)^2-4\pi r^2 = 8\pi\cdot rdr$ ainsi: $\Delta P = \frac{2\sigma}{r}$
Mesure de la tension de surface
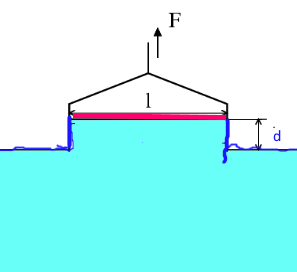
La baguette de longueur l est solevé et entraîne deux lames du liquide jusqu'au moment de la rupture , moment où la force $F$ mesurée . Ce n'est qu'au moment de la rupture que l'énergie de tension superficielle crée par les deux lames qui s'ajoutent alors à la surface libre est suffisante pour compenser l'énergie dépléyée par la force $F$ pour soulever les lames. S'il n'y avait pas de rupture, cette énergie serait inférieure au travail de $F$ Ici le principe de conservation de l'énergie joue donc le rôle esentiel! À la rupture: $\sigma \cdot \Delta A = F \cdot d$ $\sigma \cdot 2\cdot l\cdot d = F \cdot d$ $\sigma = \frac{F}{}2l$
On mesure $l$ , puis $F$ au moment de la rupture: $\sigma = \frac{F}{2l}$
Exercices
1
Expliquez pourquoi deu bulles de liquide ont tenance à se réunir pour ne former qu'une seule .
Surface totale des deux bulles: $S_2 = 2\cdot 4\pi\cdot r^2$ = $8\pi\cdot r^2$ Volume total: $V = 2\cdot\frac{4\pi r^3}{3}$ Rayon de la grande bulle: $\frac{4\pi r'^3}{3} = 2\cdot\frac{4\pi r^3}{3}$ $r'^3 = 2r^3$ $r' = 1,26 r$ Surface de la grande bulle: $S_1 = 4\pi\cdot r'^2 = 6,35\pi r^2$ La surface diminue, donc la tension aussi, ce qui est énergétiquement plus favorable `!
2

Il faut $1,8\ 10^{-4} J$ de travail pour augmenter la surface d'un film de bulle de savon de $50\ cm^2$ à $87,5\ cm^2$. Calculer la valeur de la tension superficielle de la solution savonneuse.
Une bulle de savon a deux surfaces libres, donc: Augmentation de la surface: $\Delta A = A_2 - A_1 = 2(87,5-50) × 10^{-4}\ m^2 = 74 × 10^{-4}m^2 $. Travail effectué pour cette augmentation $W = \sigma \cdot \Delta A$ $\sigma = \frac{W}{\Delta A }$ = $\frac{1,8\cdot 10^{-4}}{74 \cdot 10^{-4}}$ = $2,4\cdot 10^{-2}\frac{N}{m^2}$
3
On donne $\sigma_{eau}$ = $0,0736 \frac{N}{m}$ ; Quelle puissance faut-il développer pour transformer $6\ l$ d'eau par heure en bulles de $2\ \mu m$ de diamètre?
Nombre de bulles= Volume de l'eau / Volume d'une bulle $n = \frac{2\cdot 10^{-3}\cdot 3}{4\pi r^3}$ Surface des bulles $S=n\cdot 4\pi r^2$ Travail par heure $W = \sigma \cdot S$ Puissance $Q = \frac{W}{3600}$ ;$= \frac{0,0736\cdot 6\cdot 10^{-3}}{1\cdot 10^{-6}\cdot 3600}= 0,123\ \frac{J}{s} $