La dilatation des solides et liquides
 

     

•   Mathematiques de base
•   Physique de base
•   Chimie de base

Échelles de température Kelvin ($K$) et Celsius ($C$)

 

   Température Celsius = Température Kelvin - 273,15    $0\ K = -273,5^oC$    $273,15\ K = 0^oC$    $373,15\ K = 100^oC$

Dilatation linéaure $l-l_o$

 

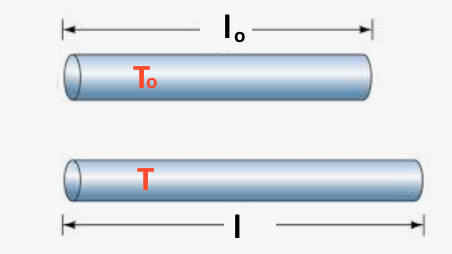
    L'alongement est proportionnel à la longueur initiale $l_o$ et l'augmentation de température $\Delta T$     Ce qui est bien compréhensible, parce que l'alongement sert justement dans les thermomètres à mesurer la variation de température!

       $l-l_o = \alpha\cdot l_o\cdot (T-T_o)$           $\Delta l$ = $\alpha\cdot l_o\cdot \Delta T$        $\alpha$ est le coefficient de dilation linéaire

Exemple

    $\alpha_{Cu} = 17\cdot 10^{-6} \frac{}{K}$     Calculer l'allongement d'une tige de cuivre de $1,8\ m$ de long à $10^o$ chauffée à $30^o$

   →   Calcul

   $\Delta l = 17\cdot 10^{-6}\cdot 1,8 \cdot 20 = 6,12\cdot 10^{-4} m$

Dilatation volumique

 

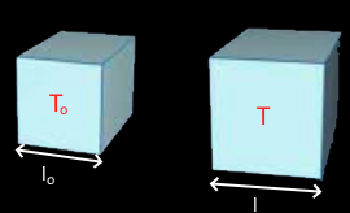
       ;$V - V_o = \beta\cdot V_o\cdot (T-T_o)$           ;$\Delta V$ = $\beta \cdot V_o\cdot \Delta T$        $\beta$ est le coefficient de dilation linéaire        $\beta\ =\ 3\alpha$

   →   Démonstration

    Voyons la figure en haut:         $\Delta V = l^3-l_o^3 = (l_o +l_o\cdot \alpha\cdot\Delta T)^3-l_o^3$     = environ $ 3\cdot \alpha\cdot l_o\cdot \Delta T$         en effet, comme $\alpha$ est très petit, $\alpha^2$ est négligeable    

Exercice

   À $0^oC$     $\rho_{Hg} = 1,36\cdot 10^{4} \frac{kg}{m^3} =\rho_1$     $\beta_{Hg} = 0,000182\frac{}{K}$     Chercher $\rho_2 =\rho_{Hg} $ à $40^o$

   →   Calcul

    $\rho_2\cdot V_2 = \rho_1\cdot V_1$    $\rho_2\cdot (V_1 + \beta \cdot V_1\cdot \Delta T) = \rho_1\cdot V_1$    $\rho_2 = \frac{\rho_1}{1+\beta \cdot \Delta T} = 1,35\cdot 10^4 \frac{kg}{m^3}$