
Formule de Torricelli



Vitesse d'écoulement
Vitesse d'écoulement:
$v^2 = 2\cdot g\cdot h$
où
$g = 9,81\frac{m}{s^2}$
au niveau de la mer
Unités de $v$ :
$\frac{m}{s}$
Théorême de Bernoulli
(Surface); $P_1\frac{m}{\rho}+\frac{1}{2}m\cdot v_1^2 + m\cdot g\cdot h_1$ =
(Orifice); $P_2\frac{m}{\rho}+\frac{1}{2}m\cdot v_2^2+ m\cdot g\cdot h_2$
en posant:
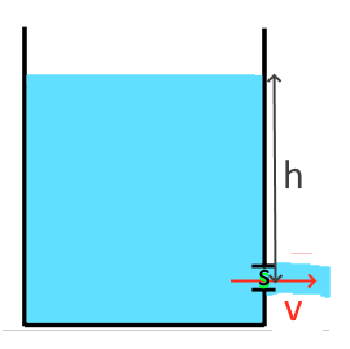
$h_2 =0$ donc $h_1= h$; (voir figure)
et évidemment:
$P_1 = P_2$; =; Pression atmosphérique
$v_1 = 0; v_2 = v$; (voir figure)
$m$; masse qui s'écoule; ; $\rho = \rho_{eau}$
En simplifiant, il reste:
(Surface); $g\cdot h$ =
(Orifice); $\frac{1}{2} v^2$
et donc:
$2\cdot g\cdot h = v^2$
On donne (voir figure en haut) $h = 2\ m$ et $s\ = 4cm^2$ Calculer le volume d'eau qui s'écoule par seconde.
$v = \sqrt{2\cdot 9,81\cdot 2 } = 6,26\frac{m}{s}$
Volume en $1\ s$: $6,26\cdot 4\cdot 10^{-4} = 2,5\cdot 10^{-3}\ m^3$
On donne (voir figure en haut) $h = 10\ m$ En outre on applique une pression $P = 2,4\cdot 10^5 Pa $ en surface
Calculer la vitesse d'écoulement.
Bernoulli (voir exercice 1):
$v^2 = 2(g\cdot h +\frac{P}{\rho_{eau}})$
$v = \sqrt{2(9,81\cdot 10 + \frac{2,4\cdot 10^5}{10^3})} = 26,0\frac{m}{s}$
Preuve
Exercices
1
2