
Théorême de Bernoulli


Théorême

L'énergie d'une portion de fluide qui s'écoule reste constante
$E$ = $ W_p$ + $E_{cin}$ + $E_{pot} $ = constante
où
$W_p$ est le travaill de la pression
$W_p = P\frac{m}{\rho}$
$E_{cin}$ est l'énergie cinétique
$E_{cin}$= $\frac{1}{2}mv^2$
$E_{pot}$ est l'énergie potentielle
$E_{pot}$= $9,81\cdot m\cdot h$
Écoulement d'un liquide de masse volumique $\rho = 0,8\frac{g}{cm^3}$ dans ce tube avec
$P_1 = 1,6\cdot 10^5 Pa; d_1 = 40\ cm;d_2 = 25\ cm; v_1 = 0,8 \frac{m}{s }; h = 6\ m$
Calculer $P_2$
Calcul de $v_2$:
$A_1v_1 =A_2v_2$ (débit !)
$v_2 =\frac{A_1v_1}{A_2 } = \frac{\pi 0,02^2 \cdot 0,8}{\pi0,0125^2}= 2,05\frac{m}{s}$
Calcul de $P_2$ (Bernoulli):
$P_2 = P_1 + \rho (\frac{v_1^2-v_2^2}{2}+9,81(0-h))$
$P_2 = 1,6\cdot 10^5 + 800(\frac{0,8^2-2,05^2}{2}-9,81\cdot 6)= 1,115\cdot 10^5 Pa $
$d_1= 30\ cm; d_2 = 15\ cm$
On a mesuré que $P_2-P_1 = 2,84\cdot 10^4\ pA $
Calculer le débit de l'eau $Q$
$v_2 =\frac{A_1v_1}{A_2}= \frac{\pi0,15^2\cdot v_1}{0,075^2}= 4v_1$
Bernoulli (aucune différence de hauteur):
$P_1-P_2 = \rho_{eau} \frac{v_1^2-(4v_1)^2}{2}$
$-2,84\cdot 10^4 = 1000 (\frac{-15v_1^2}{2}$
$v_1^2 = 3,78; v_1= 1,94\frac{m}{s} $
$Q = A_1v_1 = \pi0,15^2\cdot 1,94 = 0,137 \frac{m^3}{s}$
Une pompe monte $8\frac{l}{s} $ d'eau par un tuyau de $5\ cm$ de section à une hauteur de $16\ m$
Calculer la vitesse de remontée de l'eau et la puissance de la pompe.
En une seconde: $d =\frac{Volume}{Section}$ = $\frac{8\cdot 10^{-3}}{\pi\cdot 25\cdot 10^{-4}}$ = $4,07\ m$
En une seconde:$W = (P_2-P_1)\cdot V $ = $h \cdot \rho_{eau}\cdot 9,81\cdot V$ =
$16\cdot 1000\cdot 9,81\cdot 0,008$ = $1240\ J$
Puissance = $\frac{W}{t}= \frac{1240}{1} = 1,25 kW$
Exemple 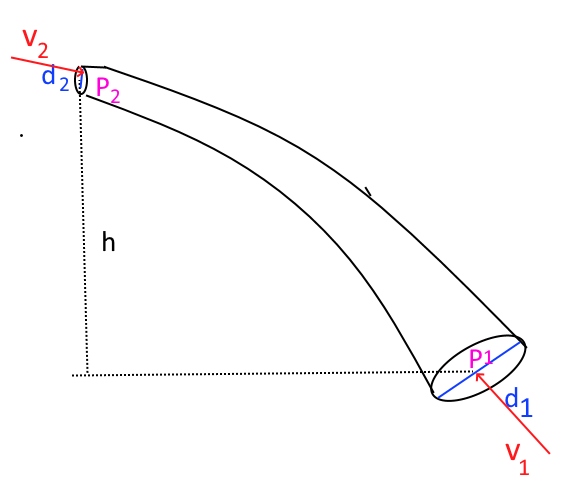
Exercices
1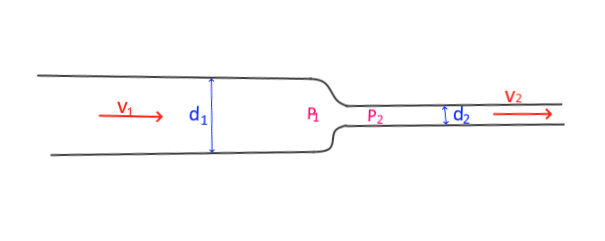
2