Vitesse, acclération, distance
Cmposantes
 

     

•   Lois de Newton
•   Mathematiques de base
•   Physique de base
•   Chimie de base

Rappel

       Accélération nulle: $a = 0$:       ________________________        Vitesse constante : $v = v_o$        Distance $d = v_o\cdot t$

      Accélération constante $a$:       ________________________        $v$ : vitesse  $v_o$ : vitesse initiale   $t$: temps :        $v = v_0 + a\cdot t$        $d = v_o\cdot t + \frac{a\cdot t^2}{2}$        $d = \frac{v^2 - v_o^2}{2\cdot a}$

Exemple 1

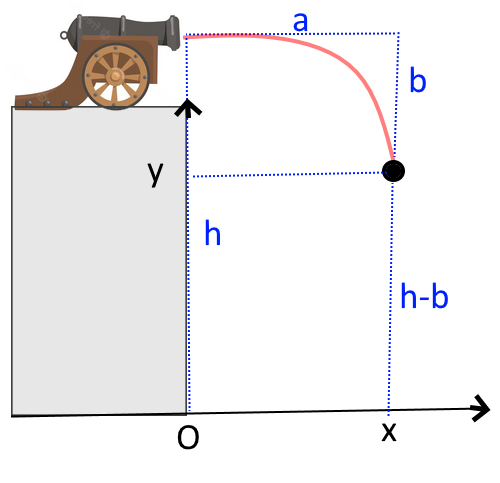
Calculer x et y après un temps t en fonction de la vitesse initiale du boulet ($\frac{m}{s}$), de t ( $s$ ) et de la hauteur h entre le sol et la bouche du canon ($ h $).    →   Calcul

$x = a = v_o \cdot t$ $b = \frac{1}{2}g t^2 = \frac{1}{2}9,81 t^2$ $y = h - b$ $y = h -\frac{1}{2}9,81 t^2$

Exemple 2

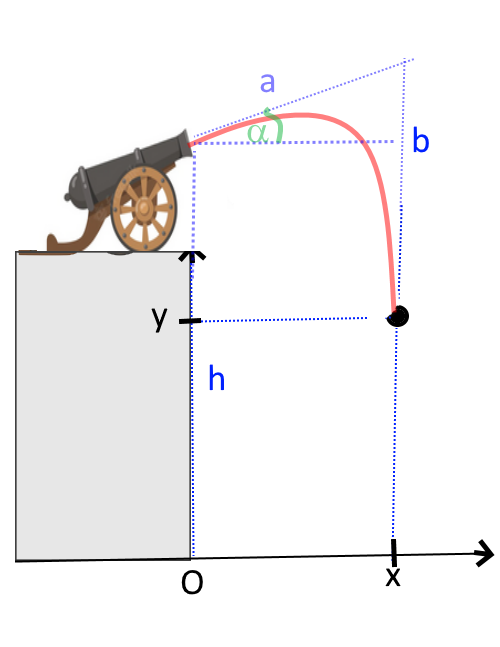
Calculer x et y après un temps t en fonction de la vitesse initiale du boulet ($\frac{m}{s}$), de t ( $s$ ) et de la hauteur h entre le sol et la bouche du canon ($ h $). et de l'angle α.    →   ici

$x = a \cdot cos \alpha = v_o \cdot cos \alpha\cdot t$ $b = -v_o \cdot sin \alpha \cdot t+\frac{1}{2}g t^2$ $y = h - b$ $y = h +v_o \cdot sin \alpha \cdot t-\frac{1}{2}9,81 t^2 $

Exemple 3

   La balle est lancée vers le haut avec $20\frac{m}{s}v_o = $    Après $2 s$ elle a atteint le point culminant et aprüs $5 s$ elle touche la mer.    La taille du bonhomme vaut $1,1 m$    Calculer la hauteur de la falaise!

   →   Calculi

Montée: $h = v_o\cdot t + \frac{a\cdot t^2}{2}$ $h = 20\cdot 2 + \frac{-9,81\cdot 2^2}{2}$ $h = 20,4 m$ Descente: $H = v_o\cdot t + \frac{a\cdot t^2}{2}$ $H =0\cdot 3 +\frac{9,81\cdot 3^2}{2}$ $H = 64,5$ Hauteur de la falaise $ = H-h-1,1 = 43 m$