Force de
frottement
 

     

•   Lois de Newton
•   Mathematiques de base
•   Physique de base
•   Chimie de base

Définition

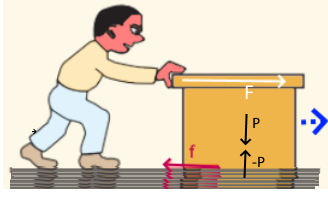
       La force de frottement ($f$) est la force qui s'oppose Partiellement au mouvement tangentiel de deux surfaces accollées. Elle est proportionnelle à la force(ici $P$) qui maintient lrd frux surfaces ensemble        $f = \mu \cdot f_P $        avec:        $f_P$: Force de cohésion       ( en haut elle est égale au poids car les surfaces sont horizontales )        $\mu $: Coeffisient de frottement dynamique

Exercice 1

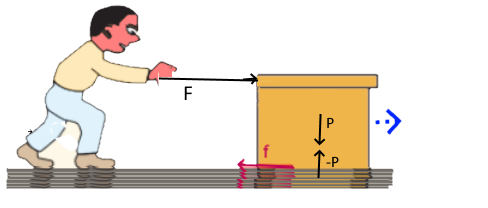
   On pousse un paquet de 30 kg sur un plan horizontal avec une force de $F =120 N$     En $5 s$ on atteint une vitesse de $1 \frac{m}{s}$     Calculer $\mu$ !

   →   Calcul

   $a = \frac{v-v_o}{t} = \frac{1-0}{5} = 0,2\frac{m}{s^2}$     $F - f = m\cdot a $     $F - \mu \cdot P = m\cdot a $     $ \mu \cdot P = F -m\cdot a $     $ \mu = \frac{F -m\cdot a}{P} $     $ \mu = \frac{ 120-30\cdot 0,2}{9,81\cdot 30} = 0,39 $

Exercice 2

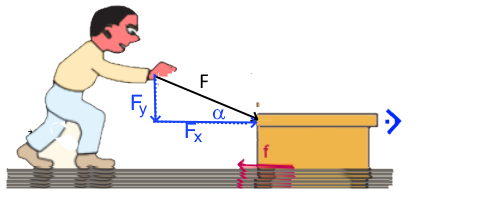
    On pousse un paquet de 18 kg sur un plan horizontal avec une force de $F =90 N$ à l'aide d'un pieu qui fait un angle de $30^o $ avec l'horizontale.     En $3 s$ on atteint une vitesse de $7,5 \frac{m}{s}$     Calculer $\mu$ !

   →   Calcul

   $a = \frac{v-v_o}{t} = \frac{7,5-0}{3} = 2,5\frac{m}{s^2}$     $F_x - f = m\cdot a $     $F\cdot cos 30 - \mu \cdot (P + F_y) = m\cdot a $     $ \mu \cdot (P + F_y) = F\cdot cos 30 -m\cdot a $     $ \mu = \frac{F\cdot cos 30 -m\cdot a}{P + F_y} $     $ \mu = \frac{F\cdot cos 30 -m\cdot a}{P + F\cdot sin 30} $     $ \mu = \frac{ 77,9-45}{221,4} = 0,149 $

Exercice 3

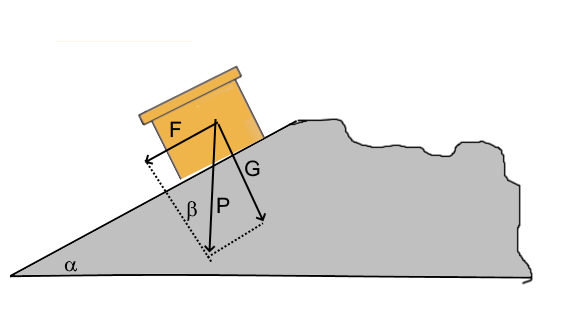
    Calculer l'accélération du paquet sachant que $\mu = 0,20$.

   →   Calcul

   $\alpha = \beta = 30^o$ (alterne-internes, puis angles d'un triangle rctangle)    $F = P sim 30$    $G = P cos 30 $    $f = \mu G = \mu P cos 30$    $m\cdot a = F - f$    $\frac{P}{9,81} \cdot a = P sim 30 -\mu P cos 30$    $a = 9,81\cdot(sin 30-0,20 cos 30)$ = $3,2\frac{m}{s^2}$