Vitesse, accélération, distance
 

     

•   Lois de Newton
•   Mathematiques de base
•   Physique de base
•   Chimie de base

 

Accélération nulle

      Accélération nulle :       $a = 0$       Vitesse constante :       $v = v_o$       Distance :       $d = v_o\cdot t$

 

Accélération constante

   Comme $a = \frac{\Delta v}{\Delta t} $ il faut que $\Delta v = v - v_o = a\cdot t $ donc    $v = v_0 + a\cdot t$ (1)    La vitesse augmente linéairement (valeur initiale : $v_o$); pente : $a\cdot z$

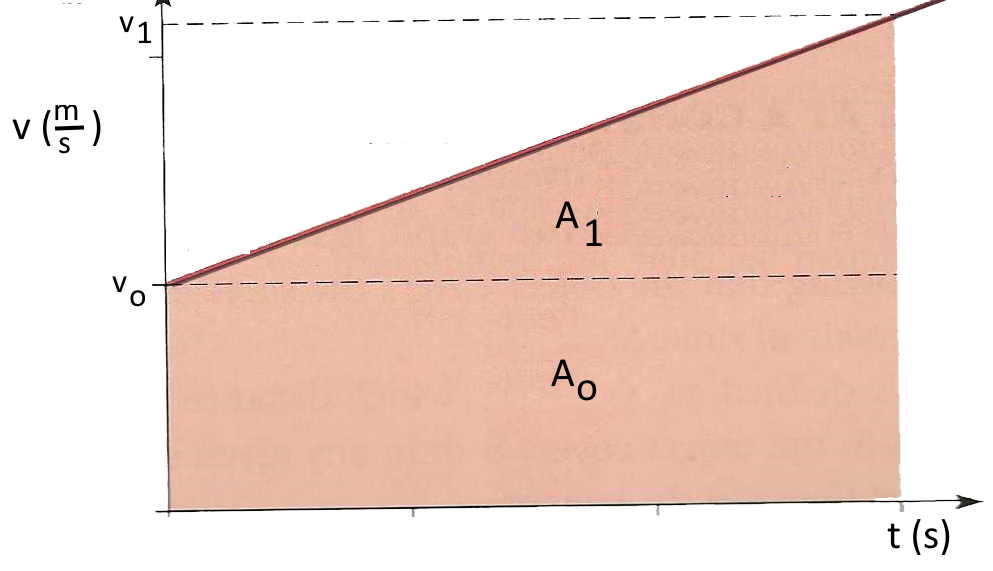
$A_o + A_1 = v_o\cdot t $ +$\frac{(v-v_o)\cdot t}{2}$ est alorsla distance parcourue en un temps $t$ $d = v_o\cdot t + \frac{(a\cdot t)\cdot t}{2}$ (2) En introdisant (1)   $t = \frac{v - v_o}{a}$ dans (2) on trouve $d = v_o\frac{v - v_o}{a} +\frac{1}{2}a (\frac{v - v_o}{a})^2$ $v^2 - v_o^2 = 2a\cdot d$

      Accélération constante $a$:       Vitesse:       $v$ : vitesse   $v_o$ : vitesse initiale   $t$: temps :        $v = v_0 + a\cdot t$       Distance:       $d = v_o\cdot t + \frac{a\cdot t^2}{2}$       $d = \frac{v^2 - v_o^2}{2\cdot a}$

Exercice 1

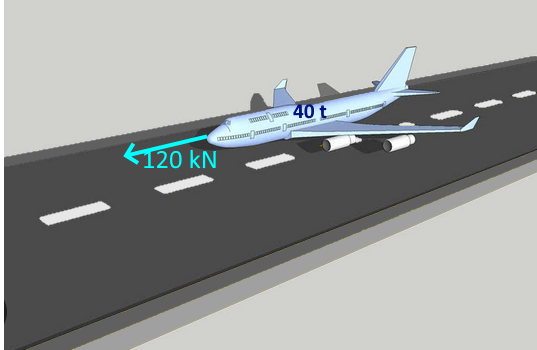
La vitesse nécessaire au décollage est de $v =60\frac{m}{s}$ . Calculer la longueur minimale de piste nécessaire.    →   ici

$a = \frac{F}{m} = \frac{120000}{40000}= 3\frac{m}{s^2} $ , $d =\frac{v^2}{2\cdot a} = \frac{3600}{6} = 600 m $

Exercice 2

Une balle est lancée verticalement en haut avec une vitesse initiale de $v_o = 14,7\frac{m}{s}$    1) Quelle sera sa hauteur maximale ?    2) Quelle sera son temps de remontée ?    →   ici

1)    Vers le haut: $a = - 9.81 \frac{m}{s^2}$    $d =\frac{v^2 - v_o^2}{2\cdot a}$    $d =\frac{0^2 - 14,7^2}{2\cdot (-9,81)}$    $d = 11,0 m$ 2)    $t =\frac{v - v_o}{a} $    $t =\frac{0 - 14,7}{-9,81} $    $t = 1,5 s $