Équilibre
des forces
 

     

•   Vecteurs
•   Mathematiques de base
•   Physique de base
•   Chimie de base

Équilibre de forces autour d'un axe

L'effet de forces qui provoquent des rotations opposées autour d'un axe s'annulle si leurs moments sont égaux dans les deux sens .

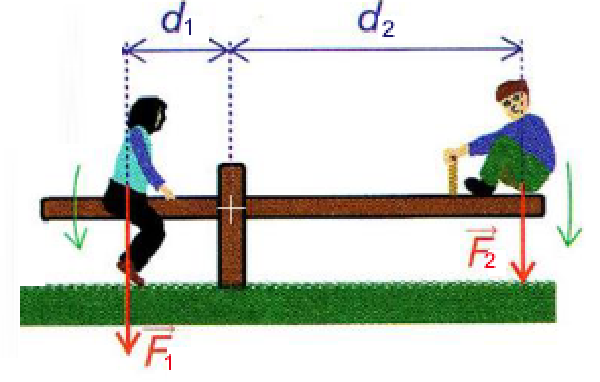
Équilibre:

$F_1 \cdot d_1 = F_2 \cdot d_2$

Exercices

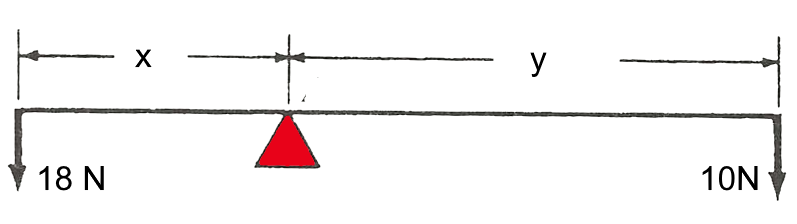
Avec une barre de 14 cm de poids négligeable il faut équilibrer les deux forces représentées. Calculer x et y !

   →  Calcul

$y = 14-x$ $18x = 10(14-x)$ $28x = 140$ $x=5 cm$ $y=14-5=9cm$

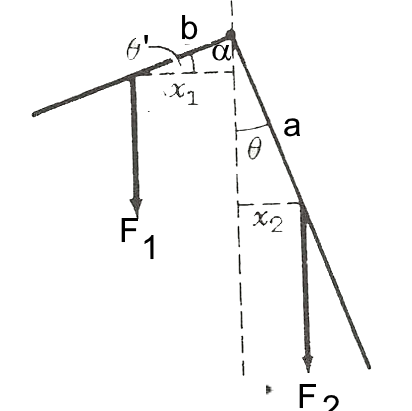
Une barre de métal eat plié à $9^o$ laissant d'un côté 6m et de l'autre 10m. Elle est suspendue au sommet de l'angle droit. Calculer $\theta$

→   →  Calcul

Soit $P$ le poids d'un mètre de barre: si $6P$ et $10P$ sont les poids des deux bras, on a: $a$= 3m et $b$=5m À l'àquilibre les moments sont égaux: $6P\cdot x_1$ = $10P\cdot x_2$ $6P\cdot 3\cdot cos\theta^,$ = $10P\cdot 5\cdot sin\theta$ $18 cos\theta^,$ = $50 sin\theta$ D'autre part $\theta = 90 - \alpha = \theta^, $( triangles rectangles) $ \frac{sin\theta}{cos\theta}$ = $ \frac{18}{50}$ $tan\theta = 0,36$ $\theta = 20^o$