Lois de
Newton et Galilée
 

     

•   Vecteurs
•   Mathematiques de base
•   Physique de base
•   Chimie de base

Première loi de Newton

La vitesse d'n corps auquel s'exerce une force résultantenulle est constante

      $\vec F\ =\ 0$     $\implies$     $v\ =\ k$ ,

       k = constante

 

Deuxième loi de Newton ( Loi fondamentle de la dynamique )

La force résultante exercée sur un corps est proportionnelle à son accélérationet a la même direction et le même sens. Le facteur de proportinalité est la masse .

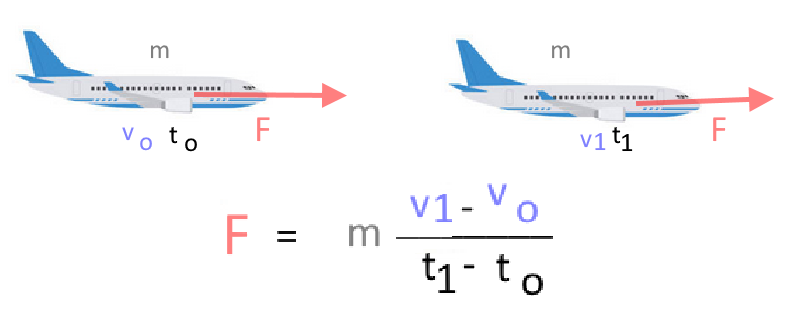
      Force = masse * accélération
      $\vec F\ =\ m \cdot \vec a$

Une masse de $1\ kg$ est soumise à une force de $10\ N$ . Quelle est son accélération? →   →  Calcul

$a=\frac{F}{m}$ $a=\frac{10}{1}$ $ = 10\frac{N}{kg} = 10 \frac{m}{s^2} $

       $1 N\ =\ 1\frac{kg\cdot m}{s^2}$

       $1 \frac{m}{s^2}\ =\ 1 \frac{N}{1kg}$

 

Troisième loi de Newton (action et réaction)

Lorsqu'un corps A exerce une force sur un autre corps B, celui-ci exercera une force oppsée sur le premier de même intensité.

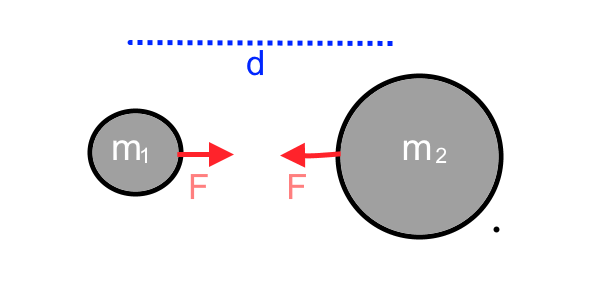
       Ici F est proportionnelle aux deux masses et inversément proportionnelle au carré de la distance:

       $ F\ =\ G \frac{m_1\cdot m_2}{d^2}$

       où la constante gravitationnelle:

       $G = 6.67 \cdot 10^{-11}\frac{N\cdot m^2}{kg^2}$

       est un facteur de proportionalité

La chute des corps: loi de Galilée

Deux corps soumis uniquement à la force gravitationnelle de la pasanteur(pas de frottementde l'air ) tombent à la même vitesse

       → Voir la chute du marteau et de la plume sur la lune

La loi de Galilée peut être déduite comme conséquence de la 3e loi de Newton:

  Près de la surface de la terre (massse $M = 5,972 × 10^{24}$ kg , rayon $r = 6,371 * 10^6 $ m) deux objets de masse $m_1= kg$ et $m_2 = kg$ sont lâchés en même temps comme Galilée l'a fait soi-disant du haut de la tour de Pise( hauteur = $d$):
 $F_1= m_1\cdot G \frac{M}{(r+d)^2}$
  $a_1= G \frac{M}{(r+d)^2}$
  $F_2= m_2\cdot G \frac{M}{((r+d)^2}$
 $a_2= G \frac{M}{(r+d)^2}$
 donc quelque soient les masses $m_1$ ou $m_2$, l'accélération est constante, donc la vitesse à l'arivée au pied de la tour doit être la même, ce que Galilée a bien découveert!
  La constante $a_1 = a_2 = g = G \frac{M}{r^2}$ vaut donc à la surface de la terre ($d$ négligeable):
 $g = 6.67 \cdot 10^{-11} \frac{5,972 × 10^{24}}{(6,371 * 10^6)^2}$
 $g = 9,81 \frac{N}{kg}$

       Poids sur la surface de la terre:

      $F = g\cdot m$
      $F = 9,81\cdot m$

      Unités:

      $F (N)$ ; $m(kg)$

Calculer le poids d'une masse $m = 100 kg $ à la surface de la lune ($M = 7,6.10^{22}kg; r= 1737,4 km$ et de la terre    →   ici

 $F_{lune} = 100\cdot 6.67 \cdot 10^{-11} \frac{7,6.10^{22}}{(1,737 * 10^6)^2}$  $F_{lune} = 168 N$  $F_{terre} = 9,81\cdot 100 = 981 N N$