







On fait réagir en milieu acide $1\; mol$ d'un alcool avec $2\; mol$ d'un acide carboxylique. La constante d'équilibre vaut $K = 4$. Calculer le nombre de moles d'ester obtenu à l'équilibre et comparez avec le résultat de l'exercice précédent.
Appelez $x$ le nombre de moles d'ester obtenu et remplissez ensuite le tableau suivant:
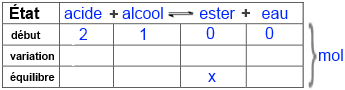
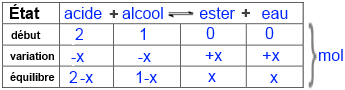
Introduisez dans l'expression de la constante d'équilibre $K$ !
$4$ = $\frac{n_{ester}n_{eau}}{n_{acide}n_{alcool}}$ = $\frac{x\cdot x}{(2-x) \cdot (1-x)}$
Résoudre l'équation ainsi obtenue !
$\frac{x\cdot x}{(2-x) \cdot (1-x)}$ $=$ $4$ $3x^2-12x+8$ $=$ $0$ $x=0,85$ La solution $x=3,15$ est évidemment à écarter, on ne peut obtenir plus d'ester qu'il n'y avait d'alcool au départ. Nombre de moles d'ester obtenus = $0,85$
La comparaison avec le résultat de l'exercice précédent illustre une loi. Laquelle ?
$0,85\;\gt\;\frac{2}{3}$ L'ajoute d'un réactif (ici l'acide) déplace l'équilibre vers la droite. (Loi de la Châtelier-Van't Hoff)