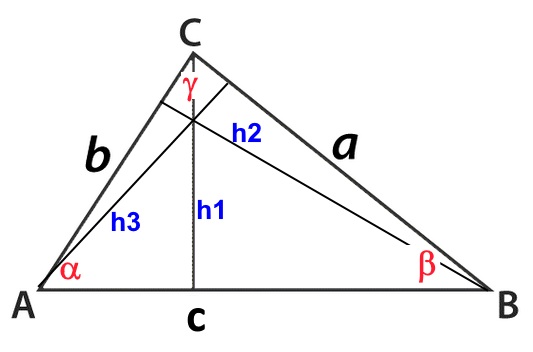
Dans un triangle quelconque:

      $\frac{sin\alpha}{a}\ =\ \frac{sin\beta}{b}\ =\ \frac{sin\gamma}{c} $ $a$ : côté opposé à $\alpha$ $b$ : côté adjacent à $\alpha$ $c$ : côté opposé à $\gamma$

Démonstration

    Soit $S$ l'aire du triangle:     $S\ =\ \frac{c\cdot h1}{2}\ =\ \frac{a\cdot h3}{2}\ =\ \frac{b\cdot h2}{2} $;     $S\ =\ \frac{c\cdot a\cdot sin\beta}{2}\ =\ \frac{a\cdot b\cdot sin\gamma}{2}\ =\ \frac{b\cdot b\cdot sin\alpha}{2} $;         Division par $\frac{abc}{2}$     $\ \frac{c\cdot a\cdot sin\beta}{abc}\ =\ \frac{a\cdot b\cdot sin\gamma}{abc}\ =\ \frac{b\cdot b\cdot sin\alpha}{abc} $;     $\ \frac{ sin\beta}{b}\ =\ \frac{sin\gamma}{c}\ =\ \frac{ sin\alpha}{a} $;

Exercices

1

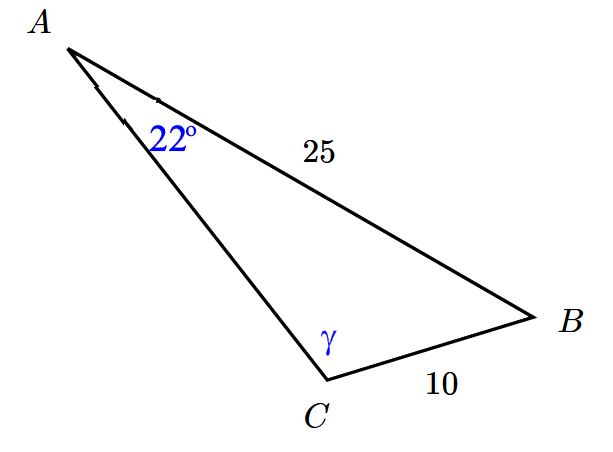    Calculer $\gamma$ !    →   Calcul

   $\frac{sin \gamma}{25}\ =\ \frac{sin 22}{10}$    $sin \gamma\ =\ \frac{25sin 22}{10}$    $sin \gamma\ =\ 159,5^o$

2

    Voir figure en haut !     $\alpha\ =\ \frac{\pi}{6} rad$;     $h\ =\ 30$     Calculer $a$!    →   Calcul

   $a\ =\ h \cdot sin\alpha\ =\ 30\cdot \frac{1}{2}\ = 15$

3

    Démontrez:     $cos^2\alpha\ + sin^2\alpha\ =\ 1$;    →   Voici:

   $cos^2\alpha\ + sin^2\alpha\ = $    $\frac{b^2}{h^2}\ +\ \frac{a^2}{h^2}= $    $\frac{a^2+b^2}{h^2} = $    $\frac{h^2}{h^2} = 1$ (→  Pythagore)