Cercle trigonométrique

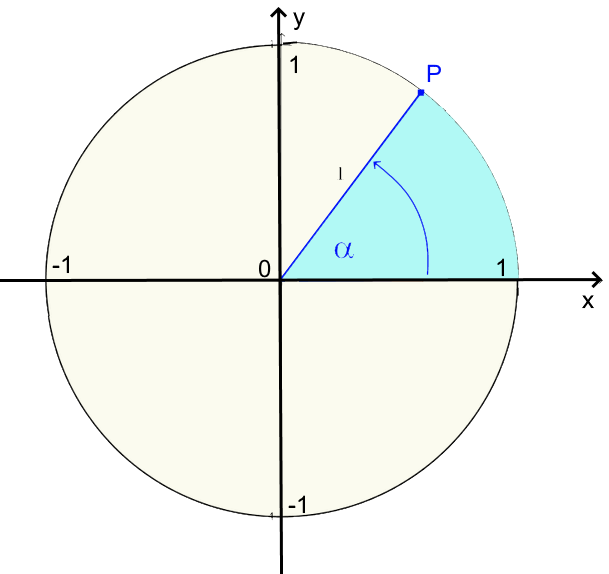
   Cercle de rayon = 1    $\alpha$ à partir de l'axe $Ox$ dans le sens indiqqué

Définition plus générale des fonctions cosinus et sinus

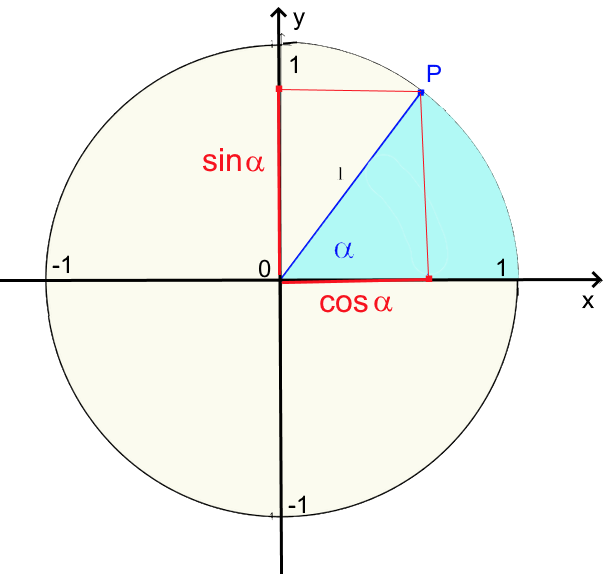
   $cos\alpha\ = $ abscisse du point $P$    $sin\alpha\ = $ ordonnée du point $P$

Généralisation 1

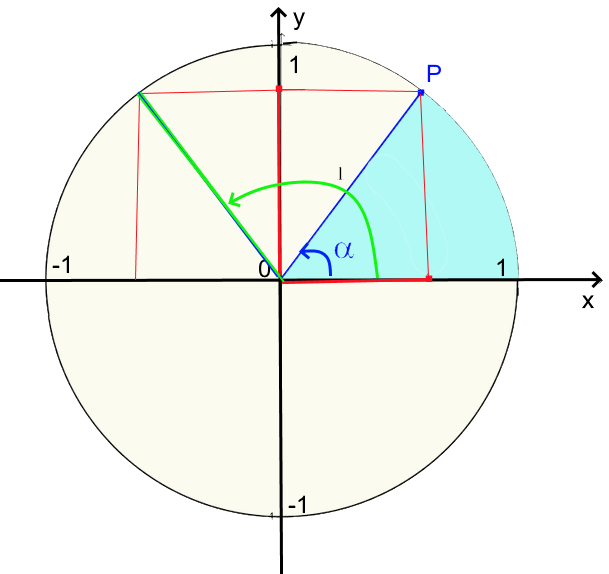
   $cos(\pi\ -\ \alpha)\ =\ -cos\alpha $    $cos(\pi\ -\ \alpha)\ =\ sin\alpha $

Généralisation 2

   $cos(\pi\ +\ \alpha)\ =\ -\ cos\alpha $    $sin(\pi\ +\ \alpha)\ =\ -\ sin\alpha $

Généralisation 3

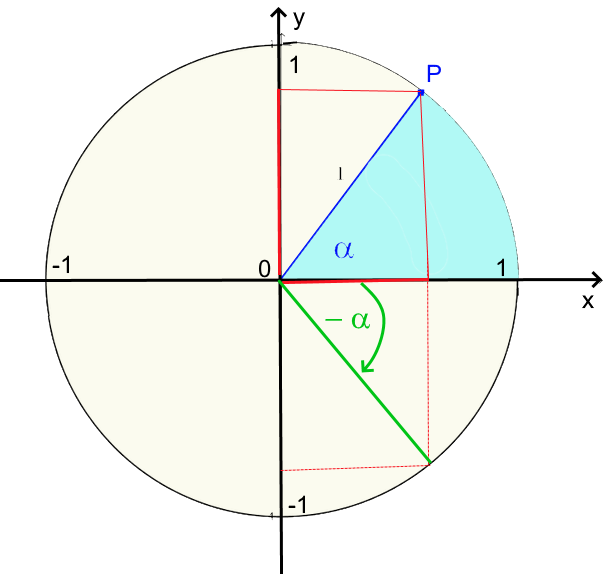
   $cos(-\ \alpha)\ =\ \ cos\alpha $    $sin(-\ \alpha)\ =\ -\ sin\alpha $

Généralisation 4

   $cos(2k\pi\ +\ \alpha)\ =\ \ cos\alpha $    $sin(2k\pi\ +\ \alpha)\ =\ \ sin\alpha $    avec    $k$ entier positif ou négatif    $tan\alpha\ =\ \frac{sin\alpha}{cos\alpha}$

Formules en $\frac{\pi}{2}$

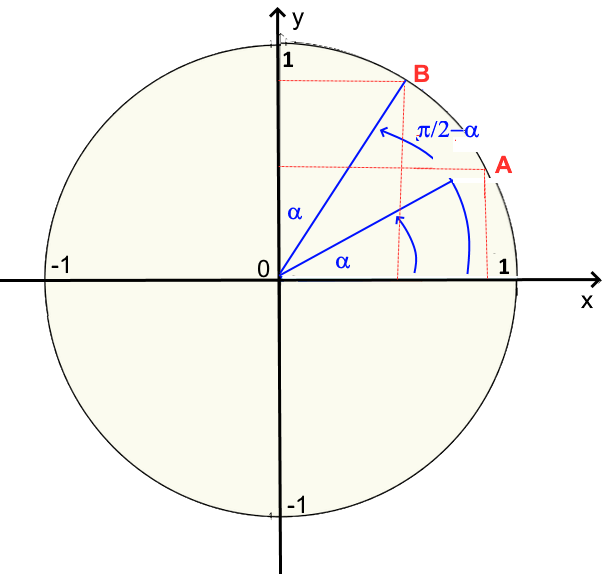
   Nous voyons:        abscisse de A = ordonnée de B    abscisse de B = ordonnée de A    et ainsi:

   $cos(\frac{\pi}{2}-\alpha)\ =\ sin\ \alpha $    $\ cos\ \alpha\ =\ sin(\frac{\pi}{2}-\alpha) $

Exercices

Voir le tebleau →  ici

1

    Calculer $cos(\frac{2\pi}{3})$ !    →   Calcul

   $cos(\frac{2\pi}{3})\ =\ cos(\pi -\frac{\pi}{3})\ =\ - cos \frac{\pi}{3}\ =\ - \frac{1}{2}$

2

    Calculer $tan(\frac{ 5\pi}{4})$ !    →   Calcul

   $cos(\frac{5\pi}{4})\ =\ cos(\pi +\frac{\pi}{4})\ =\ - cos \frac{\pi}{4}\ =\ - \frac{\sqrt{2}}{2}$    $sin(\frac{5\pi}{4})\ =\ sin(\pi +\frac{\pi}{4})\ =\ - sin \frac{\pi}{4}\ =\ - \frac{\sqrt{2}}{2}$    $tan(\frac{5\pi}{4})\ =\ \frac{sin(\frac{5\pi}{4})}{cos(\frac{5\pi}{4})}\ =\ 1$

3

    Calculer $cos(330^o)$ !    →   Calcul

   $cos(330^o)\ = cos(\frac{11\pi}{6})\ =\ cos(2\pi -\frac{\pi}{6})\ =\ cos (- \frac{\pi}{6})\ =\ \frac{\sqrt{3}}{2}$

4

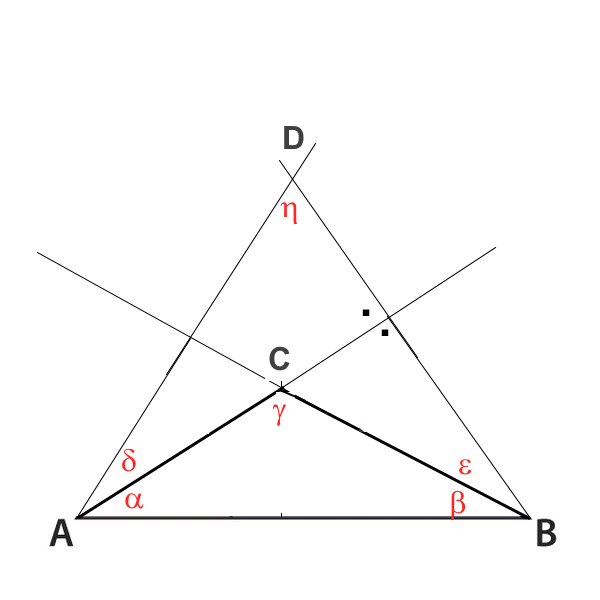
    Démontrer $in \gamma\ =\ sin \eta$    →   Voici

   On démontre d'abord que $\gamma\ =\ 180-\gamma'$:    (1) $\eta\ = 180\ -(\epsilon+\alpha)-(\delta+\beta) $    (triangle ABD)    (2) $\eta\ = 90\ -\ \epsilon$   (triangle restangle)    (3) $\eta\ = 90\ -\ \delta$    (triangle rectangle)    _____________________________________________    (5) $\eta\ =\ \alpha\ +\ \beta$ (1)(2) et (3)        (4) $\gamma\ =\ 180- (\ \alpha\ +\ \beta)$ (triangle ABC)    _____________________________________________     $\gamma\ =\ 180\ - \eta$     $sin\gamma\ =\ sin \eta$