
Trigonometry
Cosine of a sum or difference

Cosine of a sum or difference
Sum
$cos(\alpha\ +\ \beta)\ =\ cos(\alpha) cos(\beta)\ -\ sin(\alpha)sin(\beta)$
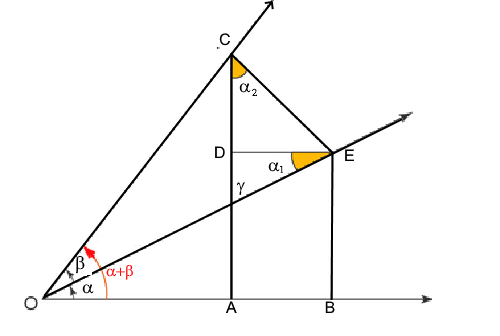
$cos(\alpha +\beta)$ $=\ \frac{OA}{OC}$ $\ =\ \frac{OB}{OC}\ -\ \frac{AB}{OC}$ $\ ==\ \frac{OB}{OC}\ -\ \frac{DE}{OC}$ $\ =\ \frac{OB}{OE}\frac{OE}{OC}-\frac{DE}{CE}\frac{CE}{OC}$ $\ =cos(\alpha) cos(\beta)\ -\ sin(\alpha)sin(\beta)$
<Difference$cos(\alpha\ -\ \beta)\ =\ cos()\alpha cos(\beta)\ +\ sin(\alpha)sin(\beta)$
$cos(\alpha\+\ (-\beta))$ $=\ cos(\alpha) cos(-\beta)\ -\ sin(\alpha)sin(-\beta)$ $=\ cos(\alpha) cos(\beta)\ +\ sin(\alpha)sin(\beta)$