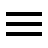
Trigonometric circle

   Circle of radius = 1    $\alpha$ from axis $Ox$ in the direction indicated

More general definition of cosine and sine functions

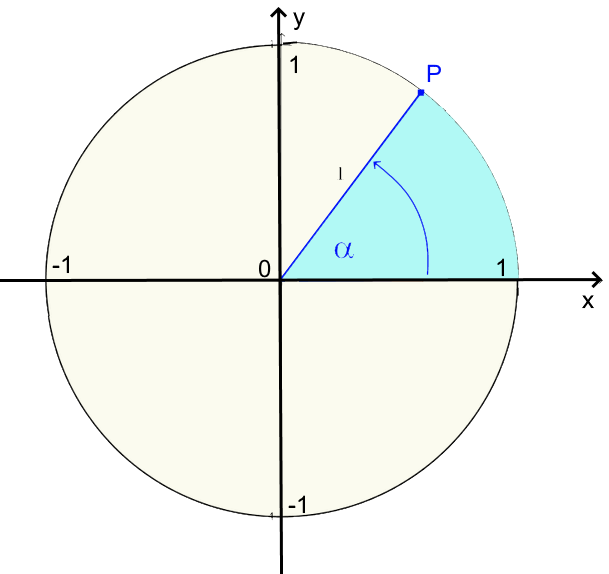
   $cos\alpha\ = $ abscissa of point $P$    $sin\alpha\ = $ ordinate of the point $P$

Generalisation 1

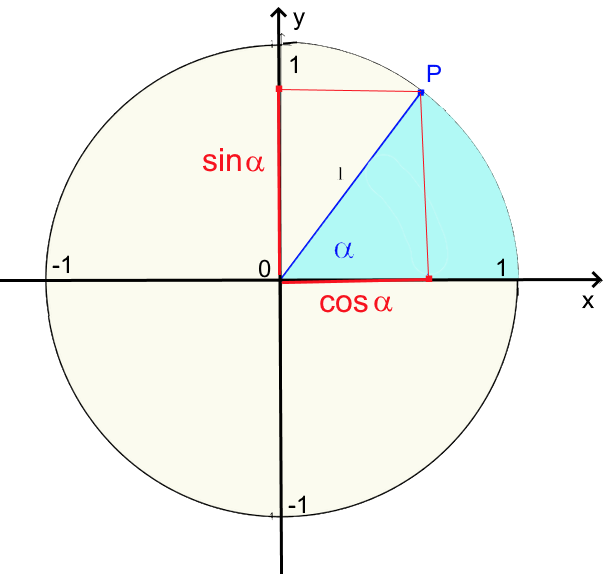
   $cos(\pi\ -\ \alpha)\ =\ -cos\alpha $    $cos(\pi\ -\ \alpha)\ =\ sin\alpha $

Generalisation 2

   $cos(\pi\ +\ \alpha)\ =\ -\ cos\alpha $    $sin(\pi\ +\ \alpha)\ =\ -\ sin\alpha $

Generalisation 3

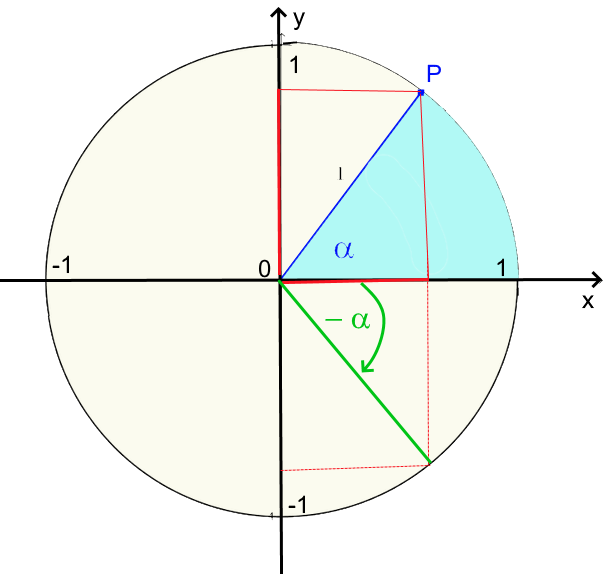
   $cos(-\ \alpha)\ =\ \ cos\alpha $    $sin(-\ \alpha)\ =\ -\ sin\alpha $

Generalisation 4

   $cos(2k\pi\ +\ \alpha)\ =\ \ cos\alpha $    $sin(2k\pi\ +\ \alpha)\ =\ \ sin\alpha $    with    $k$ positive or negative integer    $tan\alpha\ =\ \frac{sin\alpha}{cos\alpha}$

Formulas in $\frac{\pi}{2}$

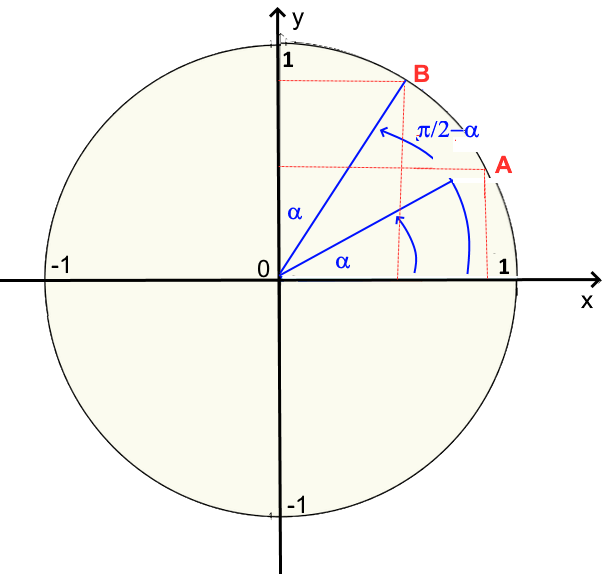
   We see:        abscissa of A = ordinate of B    abscissa of B = ordinate of A    and so:

   $cos(\frac{\pi}{2}-\alpha)\ =\ sin\ \alpha $    $\ cos\ \alpha\ =\ sin(\frac{\pi}{2}-\alpha) $

Exercises

See table →  here

1

    Calculate $cos(\frac{2\pi}{3})$ !    →   Calculation

   $cos(\frac{2\pi}{3})\ =\ cos(\pi -\frac{\pi}{3})\ =\ - cos \frac{\pi}{3}\ =\ - \frac{1}{2}$

2

    Calculate $tan(\frac{ 5\pi}{4})$ !    →   Calculation

   $cos(\frac{5\pi}{4})\ =\ cos(\pi +\frac{\pi}{4})\ =\ - cos \frac{\pi}{4}\ =\ - \frac{\sqrt{2}}{2}$    $sin(\frac{5\pi}{4})\ =\ sin(\pi +\frac{\pi}{4})\ =\ - sin \frac{\pi}{4}\ =\ - \frac{\sqrt{2}}{2}$    $tan(\frac{5\pi}{4})\ =\ \frac{sin(\frac{5\pi}{4})}{cos(\frac{5\pi}{4})}\ =\ 1$

3

    Calculate $cos(330^o)$ !    →   Calculation

   $cos(330^o)\ = cos(\frac{11\pi}{6})\ =\ cos(2\pi -\frac{\pi}{6})\ =\ cos (- \frac{\pi}{6})\ =\ \frac{\sqrt{3}}{2}$

4

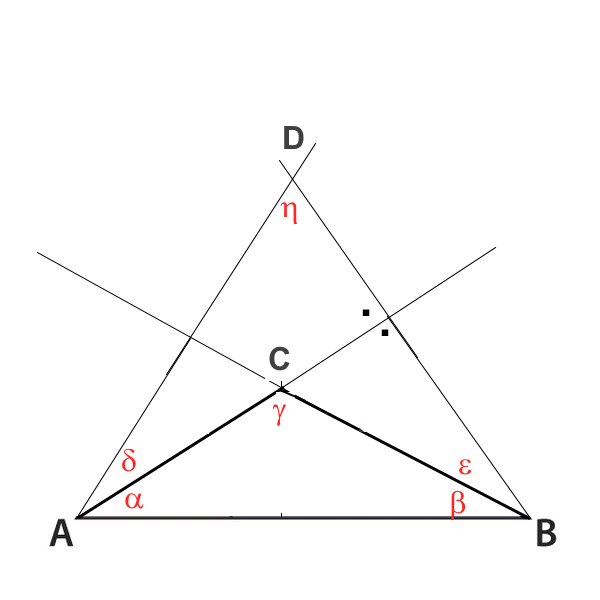
    Demonstrate $in\ \gamma\ =\ sin\ \eta$    →   Here

   We first show that $\gamma\ =\ 180-\gamma'$:    (1) $\eta\ = 180\ -(\epsilon+\alpha)-(\delta+\beta) $    (triangle ABD)    (2) $\eta\ = 90\ -\ \epsilon$   (right trianglr)    (3) $\eta\ = 90\ -\ \delta$    (right trianglr)    _____________________________________________    (5) $\eta\ =\ \alpha\ +\ \beta$ (1)(2) and (3)        (4) $\gamma\ =\ 180- (\ \alpha\ +\ \beta)$ (triangle ABC)    _____________________________________________     $\gamma\ =\ 180\ - \eta$     $sin\gamma\ =\ sin \eta$