Definitions

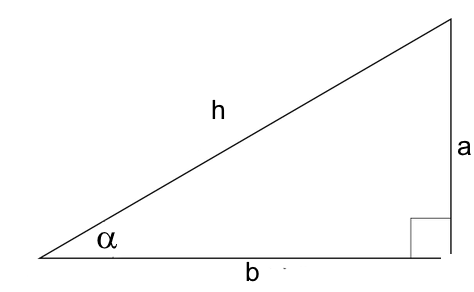
Iin the right triangle

Cosine: $cos\ \alpha\ =\ \frac{a}{h}$ Sine : $sin\ \alpha\ =\ \frac{a}{h}$ Tangent : $tan\ \alpha\ =\ \frac{a}{h}$ $h$ : hypothenuse $a$ : opposite side to $\alpha$ $b$ : adjacent side to $\alpha$ Other values: your calculator !

Exercises

1

    See figure above !     $\alpha\ =\ \frac{\pi}{3} rad$;     $h\ =\ 30$     Calculate $b$ !    →   Calculation

   $b\ =\ h \cdot cos\alpha\ =\ 30\cdot \frac{1}{2}\ = 15$

2

    See figure above !     $\alpha\ =\ \frac{\pi}{6} rad$;     $h\ =\ 30$     Calculate $a$!    →   Calculation

   $a\ =\ h \cdot sin\alpha\ =\ 30\cdot \frac{1}{2}\ = 15$

3

    Demonstrate:     $cos^2\alpha\ + sin^2\alpha\ =\ 1$;    →   Here:

   $cos^2\alpha\ + sin^2\alpha\ = $    $\frac{b^2}{h^2}\ +\ \frac{a^2}{h^2}= $    $\frac{a^2+b^2}{h^2} = $    $\frac{h^2}{h^2} = 1$ (→  Pythagore)

4

    See figure above !     Demonstrate:     $tan\alpha\ + \ =\ \frac{sin\alpha}{cos\alpha}$;    →   Here:

   $\frac{sin\alpha}{cos\alpha} = $    $\frac{\frac{a}{h}}{\frac{b}{h}}\ = $    $\frac{a}{b}\ =\ tan\alpha $