Liquides et gaz
 

     

•   Mathematiques de base
•   Physique de base
•   Chimie de base

Définition de la masse volumique $\rho$

   Masse volumique:    $\rho =\frac{m}{V}$    $m$ : masse ; $V$ volume    Unité :    $1 \frac{kg}{n^3}$

    À $4^o$:    $\rho_{eau} = 1000 \frac{kg}{m^3}$    $\rho_{air} = 1,29 \frac{kg}{m^3}$

    Exemple1:    $\rho_{Al} = 2,7 \frac{g}{cm^3} = ? \frac{kg}{m^3}$    $1000000 cm^3= 1 m^3$ ont donc une masse de $2,7\cdot1000000\ g = 2700\ kg $    $\rho_{Al} = 2700 \frac{kg}{m^3}$     Exemple2:    $5\ g$ d'un gaz occupent un volume de $7,5\ cm^3 $. $\rho\ ?$   &nbs$\rho = \frac{5\cdot 10^{-3}}{7,5\cdot 10^{-6)}} = 667 \frac{kg}{m^3} $    

Définition de la densité $d$

   Densité:    $d =\frac{\rho}{\rho_{H_2O à 4^o}}$    Unité :    sans

    Exemple:    $\rho_{Al} = 2700 \frac{kg}{m^3}$ $d\ ?$    $d_{Al}=\frac{2700}{1000}=2,7$

Définition de la pression $P$

   Pression:    $P =\frac{F}{S}$    $F$ force perpendiculaire à une surface $S$    Unité :    1 Pascal = $1 Pa =\frac{N}{m^2} $

    Exemple:     Pression exercée par une colonne de liquide de hauteur $h$ et de masse volumique $\rho\ ?$     $m = h\cdot \cdot \rho S$     $p = \frac{m}{S} = h\cdot \rho $

Exercices

1

   Un récipient vide:$600g $; plein d'eau: $50600g$; plein de glcérine: 63,6kg.    Caluler la densité de la glycérine.    →   Calcul

   $m_{eau}=50kg$    $m_{glcrérine}=63kg$    Mêmes volumes!    $d_{glcrérine} = \frac{63}{50} = 1,26$

2

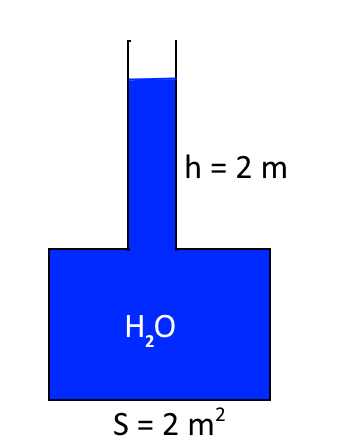
    Calculer la force que l'eau exerce sur le fond du récipient.    →   Calcul

   $P = h\cdot \rho_{eau} = 4\cdot 1000 = 4000 Pa $ ( voir Exemple en haut)    $F = P \cdot S = 4000\cdot 2 = 8000 N$

3

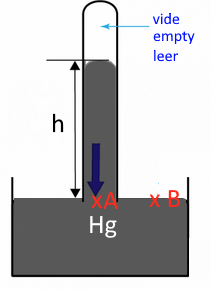
    Calculer en fonction de $h$ (en m) la pression atmosphérique ($ P_B$) qu'indique le baromètre à mercure ( $\rho = 13600 \frac{kg}{m^3}$).    →   Calcul

    Soit $S$ la section du tube (en $m^2$)     $P_b = P_A = \frac{poids Hg}{S}= \frac{9,81 masse}{S}$     = $\frac{9,81 h\cdot S\cdot \rho}{S}$     = $9,81\cdot 13600 \cdot h$      Résultat en pascal Pa !

4

    A quelle hauteur maximale peut-on siphonner de l'éther ($\rho = 7,13\frac{g}{cm^3}$) quand la pression atmosphérique correspond $ 700\ mm$ de mercure.     Voir exercice 3 !    →   Calcul

    Pression atmosphérique = Pression de l'éther     $h_{Hg}\cdot \rho_{Hg}\cdot 9,81$ = $h_{ether}\cdot \rho_{ether}\cdot 9,81$     $0,700 \cdot 13,6 \cdot 10^3$ = $h \cdot 0,713\cdot 10^3 $     $h = \frac{0,700\cdot 13,6}{0,715}=13,35\ m$