
Rotation
Moment d'inertie


Moment d'inertie( I )d'unpar corps en rotation par rapport à un axe
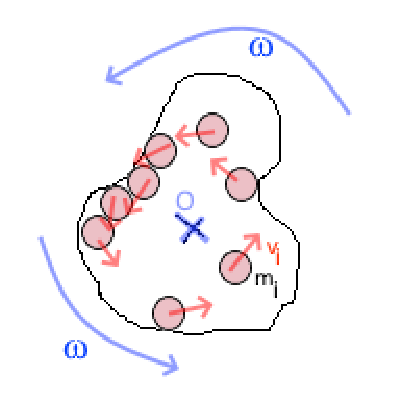
Un corps tourne avec une vitesse angulaire $\omega$ autour de son axe de rotation $O$. Imaginons que le corps est formé entièrement de très petites masses $m_i$ distantes de $r_i$ de l'axe de rotation et qui ont chacune une vitesse linéaire $v_i$. Nous définissons:
Moment d'inertie $I$ d'un corps par rapport à un axe $O$: où $r_i$ sont les distances des masse $m_i$ vers $O$$ $I = \Sigma m_ir_i^2$ Unité : $1 kg m^2$
Énergie de rotation et moment d'inertie( I )d'unpar corps en rotation par rapport à un axe
Alors son énergie cinétique de rotation vaudra: $E = \frac{1}{2}m_1 v_1 ^2 + \frac{1}{2}m_2 v_2 ^2 +\frac{1}{2}m_3 v_3 ^2 +\frac{1}{2}m_4 v_4 ^2 +\frac{1}{2}m_5 v_5 ^2 $ + etc... $E = \frac{1}{2}\Sigma m_iv_i^2$ Comme $v_i = \omega r_i$, on a : $E = \frac{1}{2}\omega \Sigma m_ir_i^2$
Énergie cinétique de rotation: $E = \frac{1}{2}\omega I $ où $\omega$ est la vitesse angulaire ($\frac{rad}{s}$) et $I$ le moment d'inertie
Moment global des forces de rotation, moment d'inertie( I ) et accélération angulaire d'un corps en rotation par rapport à un axe
Nous savons que la vitesse angulaire vaut $\omega = \frac{\theta}t{}$: d'où l'accélération angulaire : $\alpha = \frac{\theta}{t^2} = \frac{\omega}{t}$ Comme la vitesse linéaire d'une masse $m_i$ vaut $\frac{\theta \cdot r_i}{t}$ l'accélération linéaire vaut $a_l = \frac{\theta \cdot r_i}{t^2} = \frac{ \omega\cdot r_i}{t} $ Prenons maintenant une force $F_i = m_i\cdot a_l$: On a : $F_i = m_i\cdot a_l$ (Newton) $F_i = m_i\cdot a_l = m_i\cdot \frac{ \omega\cdot r_i}{t} = \alpha \cdot m_i\cdot r_i$ Pour le moment $L_i$ d'une telle force par rapport à $O$.on a: $L_i = F_\cdot r_i = \alpha \cdot m_i\cdot r_i^2 = \alpha \cdot I_i$ d'où pour l'ensemble de toutes les masses minuscules $m_i$:
Moment des forces de rotation: $L = \alpha \cdot I $ où $\alpha$ est l'accélération angulaire et $I = \Sigma m_ir_i^2$ le moment d'inertie global
Exemple
Une force de $20N$ est appliquée tangentiellement à la circonférence d'une roue de $36cm$ de rayon dont le moment d'inertie vaut $2,4kgm^2$ Trouver 1) $\alpha$ 2) $\omega$ après $4s$ 3) l'énergie cinétique de la roue après $4s$ 4) le travail effectué par la force après $4s$
1) $\alpha = \frac{F\cdot r}{I} = \frac{20\cdot 0,36}{2,4} = 3,0 \frac{rad}{s}$ 2) $\omega-\omega_o = \omega = \alpha\cdot t = 3,0\cdot 4 = 12 \frac{rad}{s}$ 3) $E = \frac{1}{2} I \omega^2 = \frac{1}{2} 2,4 \cdot 144 = 172,8 J$ 4) $W = F \cdot d = F \cdot \theta \cdot r = F \cdot \frac{1}{2} \alpha \cdot t^2 \cdot r = 20\frac{1}{2} \cdot 3,0 \cdot 16 \cdot 0,36 = 172,8 J $
Moment et accélération angulaire: $L = \alpha \cdot I $ où $\alpha$ est l'accélération angulaire et $I = \Sigma m_ir_i^2$ le moment d'inertie global
L'exemple précédent montre la relation entre moment d'une force et travail $W = F \cdot d = \frac{L}{r} \cdot d = \frac{L}{r} \cdot \theta \cdot r = L\cdot \theta $ où $r$ est bien la distance enre centre et droite portant la force puis pour la puissance : $P = \frac{W}{t} = L\frac{\theta}{t} = L\cdot \omega$
Moment, travail et puissance : Travail: $W = L\cdot \theta $ Puissance: $P = L\cdot \omega $
Exemple
Le moment d'inertie d'une roue vaut $8 kgm^2$ Quel moment doit exercer une force pour accélérer sa vitesse de $10\frac{rad}{s}$ à $20\frac{rad}{s}$ après 40 rad ?
$\theta= 40\ rad$ $E = \frac{1}{2}I(\omega^2 -\omega_0^2 )= \frac{1}{2}8\cdot(20^2 -10^2) = 1200 J$ $L\cdot \theta = E $ $L = \frac{E}{\theta}= \frac{1200}{40} = 30 Nm$
Les moments d'inerties suivants ont élé déterminés par calcul intégral:
Cylindre plein par rapport à l'axe ou disque
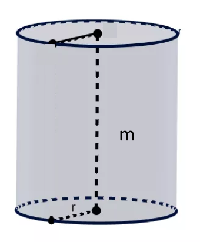 $I= \frac{1}{2}mr^2 $
Cylindre vide par rapport à l'axe ou anneau
$I= \frac{1}{2}mr^2 $
Cylindre vide par rapport à l'axe ou anneau
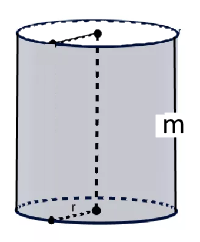 $I= mr^2 $
Rectangle par rapport à l'axe
$I= mr^2 $
Rectangle par rapport à l'axe
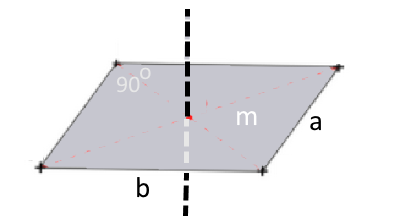 $I= \frac{1}{12}m(a^2 + b^2) $
Boule par rapport à un diamètre
$I= \frac{1}{12}m(a^2 + b^2) $
Boule par rapport à un diamètre
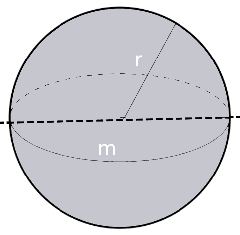 $I= \frac{2}{5}mr^2 $
$I= \frac{2}{5}mr^2 $
Exemple
Une roue de $2kg$ roule sur un plan horizontal avec une vitesse de $10 \frac{m}{s}$ Calculer son énergie!
$E_{rot} +E_{cin} =$ $\frac{1}{2}I\omega^2 +\frac{1}{2}mv^2 =$ $\frac{1}{2}mr^2\cdot \frac{v^2}{r^2}\omega^2 +\frac{1}{2}mv^2 =$ $mv^2 = 2\cdot 100 = 200 J$
Exercice
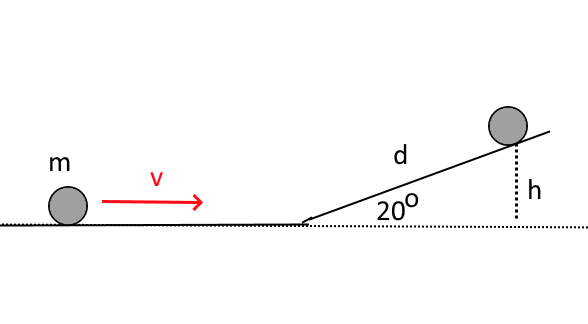
$m_{boule} = 1kg ; v = 20 \frac{m}{s}$ Calculer $h$ à l'arr^t!
Énergie au départ = $E_{rot} +E_{cin} =$ $\frac{1}{2}\frac{2}{5}m\cdot\frac{v^2}{r^2}r^2 +\frac{1}{3}mv^2$ $= 280 J$ doit vaincre la hauteur $h$: $280 = 9,81\cdot 1 \cdot h$ $h = \frac{280}{9,81} = 28,6 m$ $d = \frac{h}{sin 20} = 83,6\ m$ en négligeant le frottement !