Forces centripète
et centrifuge

Accélération centripète($a_c$) et force centripète($F_c$)

Un corps de masse m se meut avec une vitesse de valeur constante sur une trajectoire circulaire. Chercons la force qui le maintient sur sa trajectoire:

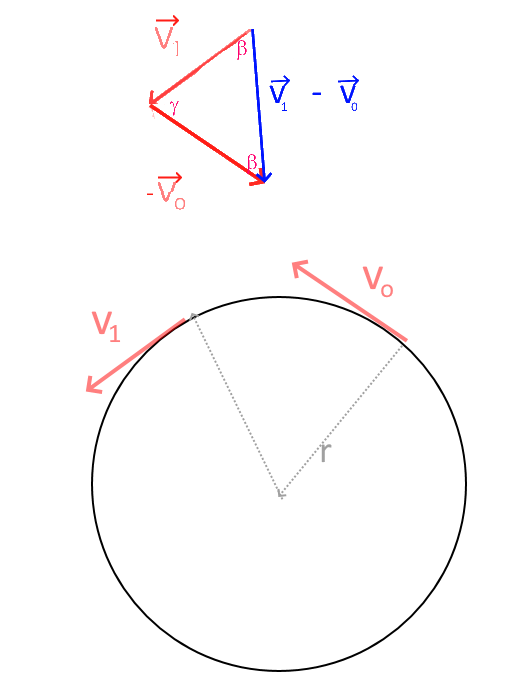
L'accélération $\vec a$ est définie par $\vec a = \frac{1}{\Delta t}\Delta \vec v$ Elle a donc même sens et même intensité que $\Delta \vec v$ Dans notre cas le vecteur $\Delta \vec v$ est représenté en haut comme base du triangle isocèle formé par les deux viteses. Si les vecteurs vitesse sont très proches ($\Delta t \rightarrow 0$) l'angle $\gamma$ au sommet de ce triangle tend vers 0 et chacun des angles égaux à sa base $\beta $ doit tendre vers $\frac{180 - 0}{2} = 90^o$ En un point du cercle, l'accélération est donc perpendiculaire à la vitesse et dirigée vers le centre du cercle. Voyons ce que vaut vaut $a$ :

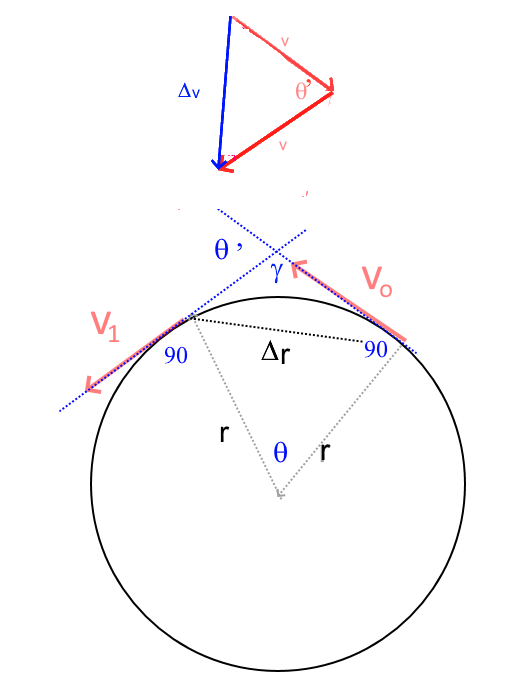
Un peu de géométrie: $\Delta r$ sur la figure est trouvé comme $\Delta v$ en haut $\gamma = 360 -90-90-\theta = 180 - \theta$(Quadrilatère: $360^o$ !) $\theta ^, = 180 - \gamma = \theta$ angle entre les deux vitesses aussi en haut Triangles isocèles semblables: $\frac{\Delta v}{\Delta r} =\frac{v}{r}$

Et puis l'accélération centripète et la force centripète : Pour un très petit espace de temps $t$ $a = \frac{\Delta v}{t} = \frac{v}{r} \frac{\Delta r}{}t$ (voir en haut) $= \frac{v}{r} \cdot v= \frac{v^2}{r}$ .et puis la force centripète: $F_c = m\cdot a_c = \frac{mv^2}{r}= m\cdot \omega^2 r$ Et enfin la 3e loi de Newton : Le corps doit exercer une force égale à la force centripète mais de sens opposé pour le maintenir sur la trajectoite $ F_f = m\cdot a_c = \frac{mv^2}{r} = m\cdot \omega^2 r$

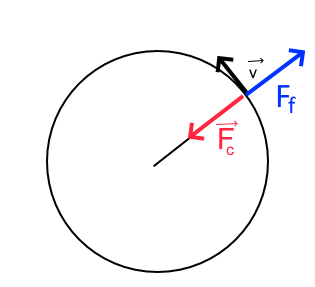
Accélération centripète $a_c = \frac{v^2}{r}$ Force centripète $F_c = \frac{m\cdot v^2}{r}$ $= m\cdot \omega^2 r$ Force centrifuge $F_f = \frac{m\cdot v^2}{r}$ $= m\cdot \omega^2 r$

Exemple 1

$\omega = 5\frac{rad}{s}$ $r = 1,5 m$ $m = 2 kg$ Calculer $v$, $a_c$ et $F_c$

$v = \omega\cdot r = 7,5 \frac{m}{s}$ $a_c = \frac{v^2}{r} = \frac{7,5^2}{1,5} = 37.5 \frac{m}{s^2} $ $F_c = m\cdot a_c = 75 N$

Exemple 2

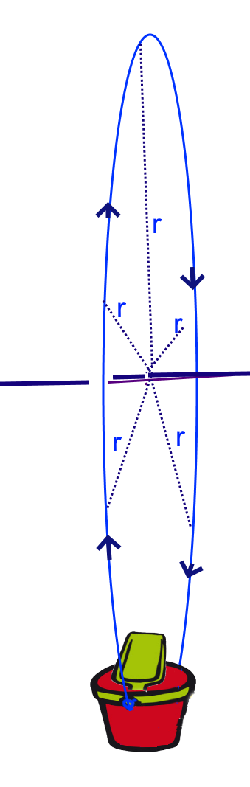
Rotation du seau dans le plan vertical attachée à un fil $r = 1 m$ Calculer la vitesse de rotation minimale pour que la pele ne tombe pas au sommet de la trajectoire!

Au sommet: Force centrifuge de la pelle = son poids $\frac{mv^2}{r} = m\cdot 9,81 $ $v = \sqrt{9,81\cdot 1} = 3,13 \frac{m}{s} $

Exemple 3

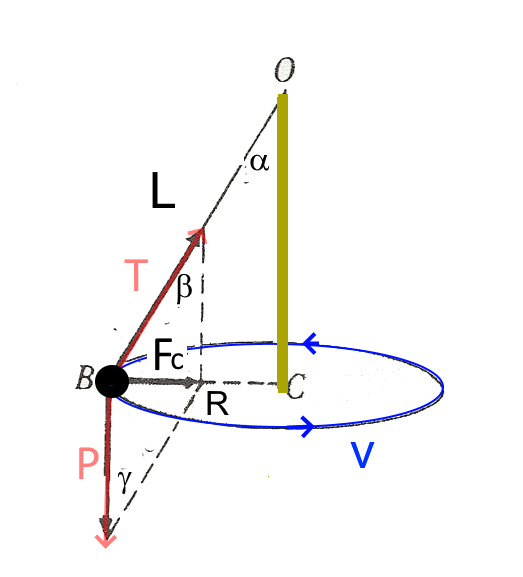
Rotation de la boule attachée au fil OB $\vec T$: Tension;$\vec P $ : Poids; $\vec F_c$: force centripète $L = 12 cm$ $\alpha = 30^o$ Calcler $v$

$\vec F_c = \vec P + vec T$ $\alpha = \beta $ (correspondants) $\beta = \gamma $ (parallélogramme) $R = 12 sin 30^o = 6 cm = 0,06 m $ $F_c =\frac{mv^2}{R} $ $P = m\cdot g$ ($g = 9,81\frac{m}{s^2}$ $F_c = tan 30^o P$ $\frac{mv^2}{0,06} = m \cdot 9,81\cdot 0,5774$ $v = \sqrt{ 9,81\cdot 0,5774\cdot0,06} = 0,583 \frac{m}{s}$

Exemple 4

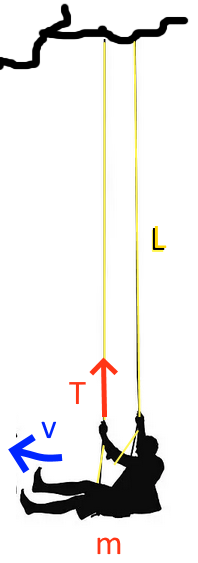
$m = 60 kg$; $L = 8 m$ Au point le plus bas: $v = 7 \frac{m}{s}$ $T$ ?