Die Gesetze von Newton und Galilei
 

Das erste Gestz von Newton

Die Geschwindigkeit eines Körpers, auf den eine feste Kraft ausgeübt wird, ist konstant

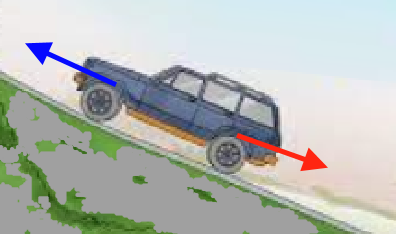
      $\vec F\ =\ 0$     $\implies$     $v\ =\ k$ ,

       k = konstant

 

Das zweite Newtonsche Gesetz (Grundgesetz der Dynamik)

Die auf einen Körper ausgeübte resultierende Kraft ist proportional zu seiner Beschleunigung und hat die gleiche Kraftlinie und Richtung. Der Proportionalitätsfaktor ist die Masse.

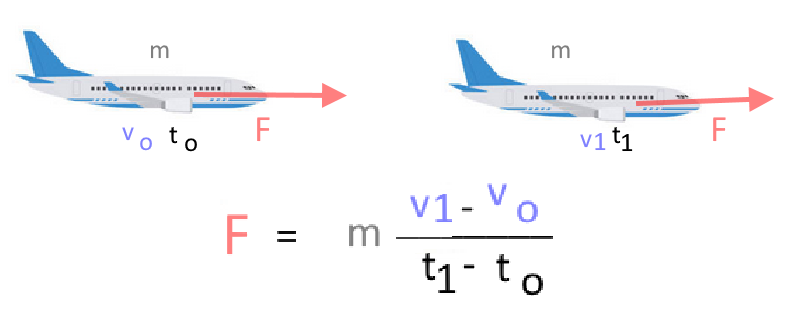
      Kraft = Masse * Beschleunigung
      $\vec F\ =\ m \cdot \vec a$

Eine Masse von $1\ kg$ wird einer Kraft von $10\ N$ ausgesetzt. Wie groß ist die Beschleunigung?    →  Rechnung

$a=\frac{F}{m}$ $a=\frac{10}{1}$ $ = 10\frac{N}{kg} = 10 \frac{m}{s^2} $

       $1 N\ =\ 1\frac{kg\cdot m}{s^2}$

       $1 \frac{m}{s^2}\ =\ 1 \frac{N}{1kg}$

 

Drittes Newtonsches Gesetz (Aktion und Reaktion)

Wenn ein Körper A eine Kraft auf einen anderen Körper B ausübt, übt dieser auf den ersten eine entgegengesetzte Kraft gleicher Intensität aus.

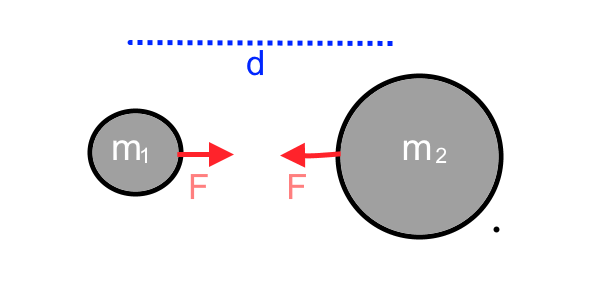
       Hier ist F proportional zu den beiden Massen und umgekehrt proportional zum Quadrat der Entfernung:

       $F\ =\ G \frac{m_1\cdot m_2}{d^2}$

       wobei die Gravitationskonstante:

       $G = 6,67 \cdot 10^{-11}\frac{N\cdot m^2}{kg^2}$

       der Proportionalitätsfaktor ist

Der Fall der Körper: Galileis Gesetz

Zwei Körper, die nur der Gravitationskraft unterliegen (keine Luftreibung), fallen mit gleicher Geschwindigkeit

       → Sehen Sie den Hammer- und Federfall auf dem Mond

Das Gesetz von Galilei kann als Folge des 3. Newtonschen Gesetzes abgeleitet werden:

  Nahe der Erdoberfläche (Masse der Erde $M\ =\ 5,972 × 10^{24}$ kg , Radius $r\ =\ 6,371 * 10^6 $ m) werden zwei Objekte der Masse $m_1\ =\ kg$ und $m_2\ =\ kg$ fallen gelassen zur gleichen Zeit wie angeblich Galileo es getan hat von der Turmspitze von Pisa aus (Höhe = $d$):
  $F_1\ =\ m_1\cdot G \frac{M}{(r+d)^2}$
  $a_1\ =\ G \frac{M}{(r+d)^2}$
  $F_2\ =\ m_2\cdot G \frac{M}{((r+d)^2}$
  $a_2\ =\ G \frac{M}{(r+d)^2}$
  Unabhängig von den Massen $m_1$ oder $m_2$ ist die Beschleunigung also konstant, also muss die Geschwindigkeit bei der Ankunft am Fuß des Turms gleich sein, was Galileo entdeckte!
  Die Konstante $a_1\ =\ a_2\ =\ g\ =\ G \frac{M}{r^2}$ gilt also an der Erdoberfläche ($d$ vernachlässigbar):
  $g\ =\ 6,67 \cdot 10^{-11} \frac{5,972 × 10^{24}}{(6,371 * 10^6)^2}$
  $g\ =\ 9,81 \frac{N}{kg}$

       Gewicht auf der Erdoberfläche:

      $F\ =\ g\cdot m$
      $F\ =\ 9,81\cdot m$

      Einheiten :

      $F (N)$ ; $m(kg)$

Berechne das Gewicht einer Masse $m\ =\ 100 kg $ auf der Oberfläche des Mondes ($M\ =\ 7.6.10^{22}kg; r\ =\ 1737.4 km$ und der Erde    →   hier

 $F_{Mond}\ =\ 100\cdot 6,67 \cdot 10^{-11} \frac{7,6*10^{22}}{(1.737 * 10^6)^2}$  $F_{Mond}\ =\ 168 N$  $F_{Erde}\ =\ 9,81\cdot 100\ =\ 981 N N$