Gleichgewicht der Kräfte
 

Kräftegleichgewicht um eine Achse

Die Wirkung von Kräften, die entgegengesetzte Drehungen um eine Achse verursachen, hebt sich auf, wenn ihre Impulse in beiden Richtungen gleich sind.

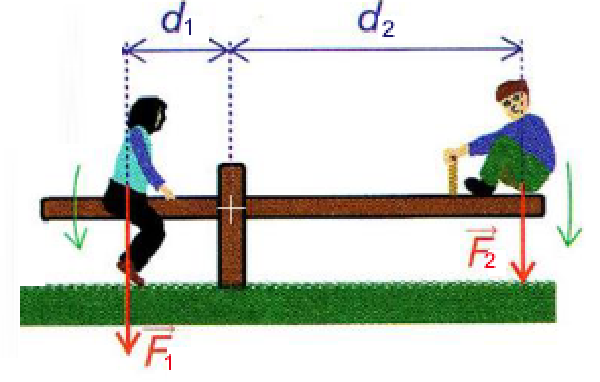
Gleichgewicht:

$F_1 \cdot d_1 = F_2 \cdot d_2$

Übungen

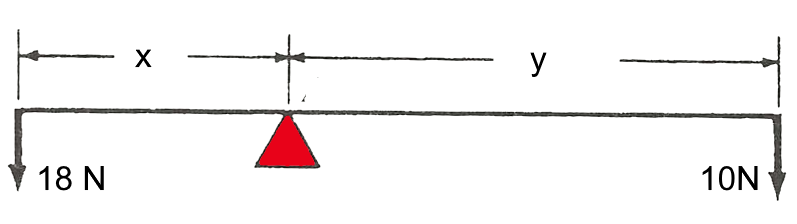
Bei einem 14 cm langen Balken mit vernachlässigbarem Gewicht müssen die beiden dargestellten Kräfte ausgeglichen werden. Berechne x und y!

→    Berechnung

$y\ =\ 14-x$ $18x\ =\ 10(14-x)$ $28x\ =\ 140$ $x=5\ cm$ $y\ =\ 14-5\ =\ 9cm$

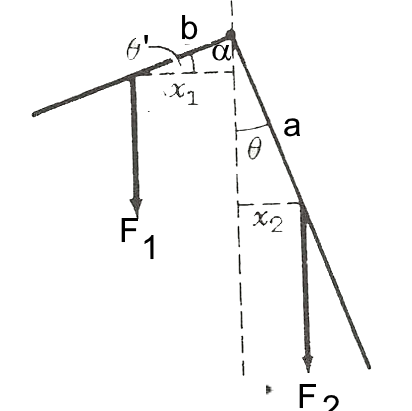
Eine Metallstange wird bei $9^o$ gebogen, wobei auf der einen Seite 6 m und auf der anderen 10 m übrig bleiben. Es wird oben im rechten Winkel aufgehängt. Berechnen Sie $\theta$

→    Berechnung

Sei $P$ das Gewicht von einem Meter Stange: Wenn $6P$ und $10P$ die Gewichte der beiden Arme sind, haben wir: $a$\ =\ 3m und $b\ =\ 5\ m$ Im Gleichgewicht sind die Momenteg leich: $6P\cdot x_1$ = $10P\cdot x_2$ $6P\cdot 3\cdot cos\theta^,$ = $10P\cdot 5\cdot sin\theta$ $18 cos\theta^,$ = $50 sin\theta$ Andererseits $\theta\ =\ 90 - \alpha\ =\ \theta^, $( rechtwinklige Dreiecke) $ \frac{sin\theta}{cos\theta}$ = $ \frac{18}{50}$ $\tan\theta\ =\ 0,36$ $\theta\ =\ 20^o$