Die Beschleunigungen
 

Definition

Die Beschleunigung eines Mobils ist die Geschwindigkeitsänderung pro Sekunde

$a\ =\ \pmb{\frac{\Delta v}{\Delta t}}$

Beispiele

Auf den folgenden Bildern stellt ein Strich einen Meter dar:

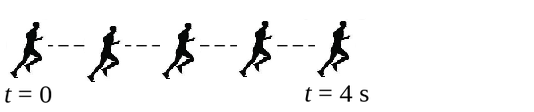
Auf allen Ein-Sekunden-Leerzeichen: $v\ =\ \frac{3m}{1s}\ =\ 3 \frac{m}{s}$ Also auf jedem Intervall relativ zum vorherigen: $\Delta v\ =\ 0 \frac{m}{s}$ und so: $a = \frac{\Delta v}{\Delta t}\ =\ 0$

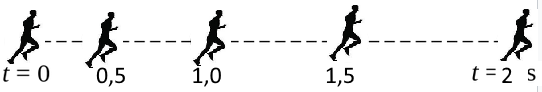
In Abständen von einer halben Sekunde: 1) $v = \frac{3 m}{ 0,5 s}\ =\ 6 \frac{m}{s}$ 2) $v = \frac{5 m}{ 0,5 s}\ =\ 10 \frac{m}{s}$ 3) $v = \frac{7 m}{ 0,5 s}\ =\ 14 \frac{m}{s}$ 4) $v = \frac{9 m}{ 0,5 s}\ =\ 18 \frac{m}{s}$ Also auf jedem Intervall relativ zum vorherigen: $\Delta v\ =\ 4 \frac{m}{s}$ und damit bleib tdie Beschleunigung $a\ =\ \frac{\Delta v}{\Delta t}\ =\ 4\frac{m}{s^2} $ hier konstant.