Acid-base titration
Tutorial 13
pH during titration of a weak acid by a strong base
Schematic:
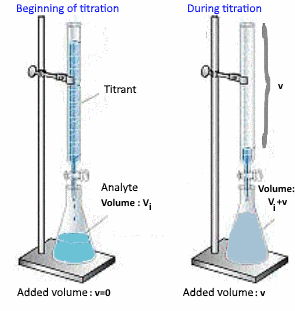
Determining the base volume $ V_e $ added at the equivalent point
$ n_{added \;base } = n_{initial \; acid} $
$ V_e \cdot c_{base} = V_i \cdot c_{acid} $
Hence $ V_e $
pH by volume $ v $ of base added
$ v = 0 $
pH of a weak acid of molarity $ c_{acid} $:
$ x = [H_3O^+] $
$ x ^ 2 + c_{acid} x-c_{acid} K_a = 0 $
Etc.
$ v \lt V_e $
Determine the number of moles of acid $ n_a $ which have not yet reacted as well as the number of moles of weak base $ n_b $ formed.
pH of buffer
$ pH = pK_a + log\frac{n_b}{n_a} $
$ v = V_e $
pH of a weak base, molarity: $ c_b $:
The number of moles of weak base at this time $ n_b $ $ = $ $ n_{added \; base} $ $ = $ $ n_{initial \; acid} $
Then: $ c_b = \frac{n_b}{V_i + V_e} $
Then
$ x = [OH^-] $:
$ x^2 + c_bx-c_bK_b = 0 $
etc...
$ v \gt V_e $
Determine the numbers of strong base moles $ n_b $ in excess
$ pH = 14 + log \frac{n_b}{V_i + v} $
$20\;mL\; CH_3COOH \;0,05\;M$ sont titrés par $NaOH\;0,1\;M$
Calculer le volume $V_e$ de base ajoutée au point équivalent
For answers, use (possibly several times) the arrows ↑ Down! and ↓ Up!
Complete please this question before moving on to the next one!
$V_e\cdot c_{base}=V_i\cdot c_{acide}$
$V_e\cdot 0,1=0,020\cdot 0,05$
$V_e=0,010\;L$
