





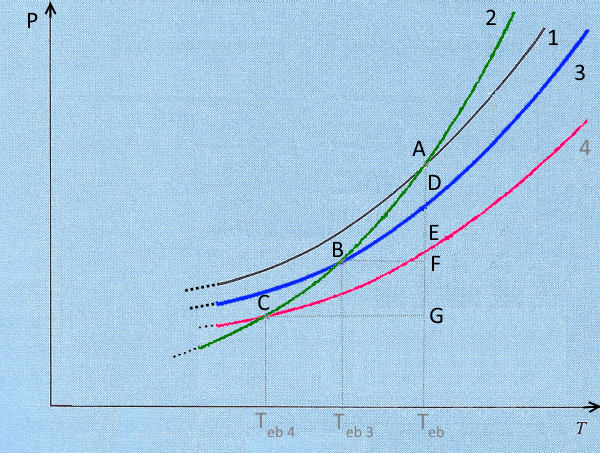
This diagram shows - Saturation vapour pressure curves of the liquid solvent $1$ and corresponding solid $2$ (see → here) - The saturation vapour pressure curves of two solutions: $s$ with mole fraction of solute $X_s$ (curve $3$) and $S$ with mole fraction of solute $X_S$ (curve $4$)
For dilute solutions, most of the previous diagram plays in a very small portion of temperatures where the curves $ 1,2,3,4$ can almost be considered to be linear:
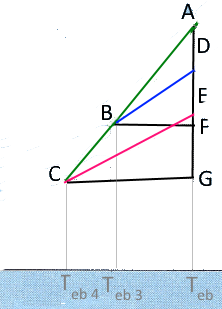
With this heuristic approach, we may use elementary geometry: Similar triangles $ABD$ and $ACE:$ $\frac{AB}{AC}=\frac{AD}{AE}\,(1)$ Similar triangles $ABF$ and $ACG:$ $\frac{AB}{AC}=\frac{BF}{CG}\,(2)$ Raoult´s law (non-volatile solute!): $AD=X_sP\,(3)$ $AE=X_SP\,(4)$ where $P$ represents the saturation vapour pessure of the solvent at its boiling temperature $T_{eb}$ Noticing that $BF=\Delta T_{eb\;s}$ and $CG=\Delta T_{eb\;S}$, and combining the preceding equations, we find: $\frac{\Delta T_{eb\;s}}{\Delta T_{eb\;S}}=\frac{X_s}{X_S}$
The decrease of the melting temperature of a dilute solution of an ideal non-volatile solute $A$ is proportional to the mole fraction of solute : $\Delta T=K\cdot X_A$ (**)
Quantities
A $0,1\;M$ dilute aqueous solution of glucose contains per liter $55.5$ moles water and only $0,1$ mole glucose!
Approximation
For a dilute solution of non-volatile solute $A$ in solvent $B$ , neglecting the number of moles of solute $A$ in $X_A$: $X_A$ $=$ $\frac{n_A}{n_A+n_B}$ $\approx $ $\frac{n_A}{n_B}$ $= $ $\frac{M_B\;n_A}{m_B}$ $= $ $\frac{M_B}{1000}\frac{1000\;n_A}{m_B}$ $=$ $\frac{M_B}{1000}\mu_A$ where $\mu_A$ is the molality of $A$ $M_B$ is the molar mass of $B$ $n_A$ are the number of moles of $A$ $n_B$ are the number of moles of $B$ $m_B$ is the mass of $B$ expressed in grams (**) gives in that case: $\Delta T$ $=$ $K\cdot\frac{M_B}{1000}\mu_A$
The decrease of the melting temperature of a dilute solution of an ideal nonvolatile solute $A$ is proportional to the molality of the solute: $\Delta T=K_{fus}\cdot \mu_A$ $K_{fus}$ is the cryoscopic constant which depends on the solvent
Melting temperatures and cryoscopic constants $\frac{^o}{mol}$
| Solvent | Nom | $t_{fus}$ | $K_{fus}$ |
| CH3CO2H | Acetic acid | $16.604$ | $3.90$ |
| CH3COCH3 | Acetone | $-95.35$ | $0.850$ |
| C6H5NH2 | Aniline | $-6.3$ | $5.87$ |
| C6H6 | Benzene | $5.5$ | $4.90$ |
| CS2 | Carbon disulfide | $-111.5$ | $3.83$ |
| CCl4 | Carbon tetrachloride | $-22.99$ | $30.0$ |
| CHCl3 | Chloroforme | $-63.5$ | $4.70$ |
| C6Hl2 | Cyclohexane | $6.55$ | $20.0$ |
| (C2H5)2O | Diethylether | $-116.2$ | $1.79$ |
| C10H8 | Naphtalene | $80.55$ | $6.80$ |
| C6H5NO2 | Nitrobenzene | $5.7$ | $7.00$ |
| C6H5OH | Phenol | $43$ | $7.27$ |
| C2H5OH | Ethanol | $-117.3$ | $1.99$ |
| H2O | Water | $0.0$ | $1.86$ |
Examples
Solution $s$ contains $0.124\; mol$ of a non-volatile solute in $250\; g$ d’eau. Calculate its melting temperature $T_s$.
Solution $s$ contains $0.124\; mol$ de magnesium chloride $(MgCl_2. \alpha=0.85)$ in $250\; g$ water. Calculate its melting temperature $T_s$.
Exercises Try them → here