





According to the law of Raoult, → the saturation vapour pressure diagram $P_s(T)$ of such a solution is as follows:
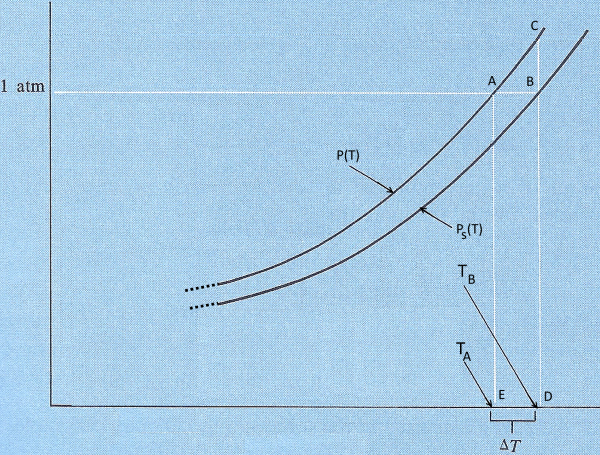
As the function $P(T)$ is (obviously) continuous and differentiable in the diagram portion represented, we can use the mean value theorem: $P(T_B)-P(T_A)$ $=$ $P^{`}(T_i)(T_B-T_A)$ where $P^{`}(T_i)$ is the derivative at a point intermediate between$T_A$ and $ T_B$, therefore equal to a constant $k$ Seen on the diagram $DC-EA$ $=$ $k(T_B-T_A)$ $BC$ $=$ $k(T_B-T_A)$ $P(T_A)-P_s(T_A)$ $=$ $k(T_B-T_A)$ $P(T_A)-X_B\;P(T_A)$ $=$ $k(T_B-T_A)$ (*) $P(T_A)(1-X_B)$ $=$ $k(T_B-T_A)$ $X_AP(T_A))$ $=$ $k(T_B-T_A)$ $(T_B-T_A)$ $=$ $\frac{P(T_A)}{k}X_A$ where $P(T_A)$ $= $ $1 \;atm$ $(T_B-T_A)$ $=$ $\frac{1}{k}X_A$ (**)
The increase in the boiling temperature of an ideal dilute solution of a nonvolatile solute $A$ is proportional to the mole fraction of solute : $\Delta T=K\cdot X_A$
Quantities
Dilute $0.1\;M$ solution of glucose in water contains per liter $55.5 $ moles of water and only $0.1$ mole of glucose!
Approximation
Given a dilute solution of a solute $A$ and solvent $B$, neglecting the number of moles of solute $A$ in $X_A$: $X_A$ $=$ $\frac{n_A}{n_A+n_B}$ $\approx $ $\frac{n_A}{n_B}$ $= $ $\frac{M_B\;n_A}{m_B}$ $= $ $\frac{M_B}{1000}\frac{1000\;n_A}{m_B}$ $=$ $\frac{M_B}{1000}\mu_A$ where $\mu_A$ is the molality of $A$ $M_B$ is the molar mass of $B$ $n_A$ are the number of moles of $A$ $n_B$ are the number of moles of $B$ $m_B$ is the mass of $B$ expressed in grams (**) gives in that case: $\Delta T$ $=$ $K\cdot\frac{M_B}{1000}\mu_A$
The increase in the boiling temperature of an ideal dilute solution of a nonvolatile solute $A$ is proportional to the molality of the solute : $\Delta T=K_{eb}\cdot \mu_A$ $K_{eb}$ is the ebullioscopic constant which depends on the solvent
Boiling temperatures and ebullioscopic constants in $\frac{^o}{mol}$
| Solvent | Nom | t(eb) | $K_{eb}$ |
| CH3CO2H | Acetic acid | $117.9$ | $3.07$ |
| CH3COCH3 | Acetone | $56.2$ | $1.71$ |
| C6H5NH2 | Aniline | $184.13$ | $3.22$ |
| C6H6 | Benzene | $80.1$ | $2.53$ |
| CS2 | Carbon disulfide | $46.2$ | $2.37$ |
| CCl4 | Carbon tetrachloride | $76.5$ | $4.95$ |
| CHCl3 | Chloroforme | $61.2$ | $3.66$ |
| C6Hl2 | Cyclohexane | $80.74$ | $2.79$ |
| (C2H5)2O | Diethylether | $34.5$ | $1.82$ |
| C10H8 | Naphtalene | $218$ | $5.8$ |
| C6H5NO2 | Nitrobenzene | $210.8$ | $5.26$ |
| C6H5OH | Phenol | $181.75$ | $3.04$ |
| C2H5OH | Ethanol | $78.5$ | $1.22$ |
| H2O | Water | $100.0$ | $0.512$ |
Examples
1) Solution $s$ contains $0.124$ mol of a non-volatile solute in $250\; g$ water. Calculate its boiling temperature $T_s$.
2) Solution $s$ contains $0.124$ mol magnesium chloride $(MgCl_2. \alpha=0.85)$ in $250\; g$ water. Calculate its boiling temperature $T_s$.
Exercises To try → here