







In an acid medium $1\; mol$ of an alcohol reacts with $2\; mol$ of a carboxylic acid. The equilibrium constant is $K = 4$.
Calculate the number of moles of ester obtained at equilibrium and compare the result with the previous exercise.
Call $x$ the number of moles of ester obtained and then fill in the following table:
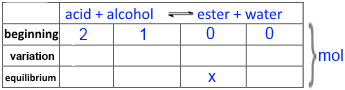
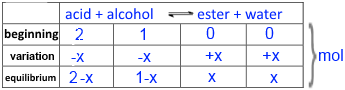
Introduce into the expression of the equilibrium constant $K$ !
$4$ = $\frac{n_{ester}n_{eau}}{n_{acide}n_{alcool}}$ = $\frac{x\cdot x}{(2-x) \cdot (1-x)}$
Solve the resulting equation!
$\frac{x\cdot x}{(2-x) \cdot (1-x)}=4$ $3x^2-12x+8$ $=$ $0$ $x=0.85$ The solution $x=3.15$ is obviously to avoid, we cannot get more ester than there was alcohol at the beginning. Number of moles of ester obtained = $0.85$
The comparison with the result of the previous exercicse shows a law. Which one?
$0.85\;\gt\;\frac{2}{3}$ The addition of a reagent (the acid here) shifts the equilibrium to the right. (Law of Van't Hoff- Le Châtelier)