






Another unexplained fact in the early 20th century was ...
If we take as a light source an element heated to a high temperature , spectral lines appear in the visible light spectrum.

What should be the origin of these lines?

Niels Bohr
The Danish physicist Niels Bohr was thinking about the spectral lines of hydrogen. Each line was derived from a photon of a fixed wavelength emitted by the atom. According to Planck's formula $ E_{photon}$ $=$ $ h\nu \;(7)$ the energy of all the photons that produce a given line should be exactly the same. But where did this energy come from and why was it the same? Bohr assumed that the H atom would have circular orbits where the electron could go around in circles. On each orbit, the electron would have a well defined energy, the energy on a remote orbit $E_2$ being higher than the energy on a$E_1$ orbit close the nucleus. (Indeed, to go from orbit to orbit far closer, the electron should perform work under the influence of the attractive force of the nucleus and therefore lose energy.) Bohr also assumed the electron, by falling from a distant orbitin an orbit close to the nucleus would loose energy $ E_2 -E_1$to the outside of the atom as a photon.
:
Quantum jump of the electron from the 4 th orbit the 1 st
Bohr proposed to recover the experimental spectrum of the hydrogen atom by reasoning on his hypothesis: He had to determine the energy of the electron on each orbit . Then it would be easy to find the position of the lines using Planck's formula. Classical physics led Bohr to the following:
Coulomb force between electron and nucleus of the atom:
The nucleus of the H atom consists of a single proton. It has the charge $ e $ $=$ $ 1.6\cdot 10^{- 19} C $ . The electron has the charge $ - e$ $=$ $ -1.6\cdot10^{-19} C $. These two charges are separated by $r$ = radius of the orbit of electron . The electron is attracted to the nucleus with the Coulomb force: $ F_1 $ $=$ $k \frac{e^2}{r^2} $, with $ k $ $=$ $ 9.0\cdot10^9\frac{Nm^2}{C}^2 $
Centrifugal force exerted on the electron:
The electron moving with a speed $ v $ in a circular orbit of radius $ r $ experiences a centrifugal force equal to: $ F_2$ $=$ $\frac{mv^2}{r} $, with $m$ $=$ $9.11\cdot 10^{- 31}\; kg$
Energy of the electron in the atom
The energy of a material system is work (force $\cdot $ displacement) that the system can do.
Potential energy:
In the H atom the single electron located at a distance $ r $ from a proton has energy because it can provide work (Coulomb Force $\cdot$ distance to nucleus) being attracted by the nucleus. Physicists show that we can write this energy in the form: $ E_{k}$ $=$ $-k\frac{e^2}{r} $ As we expect, we see that while increasing the distance from the nucleus, the energy increases. At infinite distance from the nucleus, the potential energy is (arbitrarily) set to 0, which is the maximum value!
Kinetic Energy
In the H atom the electron moving with a velocity $v$ has energy, for example as it can bump into another particle colliding with it. Physicists show that we can write this energy in the form: $ E_{cin}$ $ =$ $\frac{mv^2}{2} $
One single equation
So classical physics provides only a single equation between the unknowns $v$ and $r$: Coulomb force = Centrifugal force $k\frac{e^2}{r^2}$ $ =$ $\frac{mv^2}{r} $
To determine $v$ and $r$, it must be found a second equation between these unknowns invoking the numbernof the orbit. Bohr knew from the spectra the values of $\Delta E $ , so he deliberately imagined a second equation leading to these values: $mvr$ $ =$ $\frac{nh}{2\pi} \;(*)$ In → combining with the above equations, Bohr found the following result:
Energy of the electron in orbit of (quantum) number $n$: $E_n$ $=$ $-\frac{A}{n^2}$ with A = $2.18\cdot 10^{-18} \;(**)J $
Here is a diagram of the energy states (energies of the electron in the orbital) in the hydrogen atom:
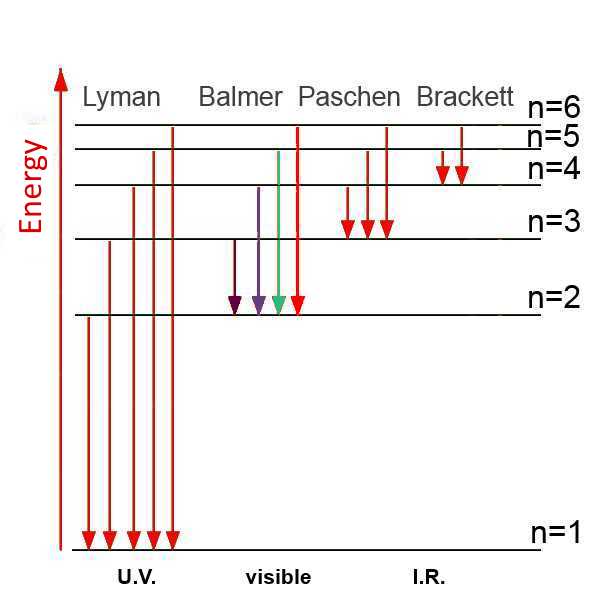
The passage of the electron from state$ n$ $ =$ $n_2$ to the state $ n$ $ =$ $ n_1 $ causes a loss of energy of (**): $ E_{n_2}$ $ -$ $ E_{n_1}$ = A $(\frac{1}{n_1^2} $ $-$ $\frac{1}{2^n_2}) $ This energy is released as a photon: $ h\nu$ = A $(\frac{1}{n_1^2} $ $-$ $\frac{1}{n_2^2}) $ so: $\nu$ $ =$ $\frac{A}{h}(\frac{1}{n_1^2}-\frac{1}{n_2^2})$ $\lambda$ $ =$ $\frac{c}{\frac{A}{h} (\frac{1}{n_1^2} -\frac{1}{n_2^2})} $
For the passage of $ n_2$ $ =$ $3$ to $ n_1$ $ =$ $ 2$ , the latter formula allows for example the calculation (!!) of a wavelength of the photon $\lambda $ = $\frac{3\cdot 10^8}{\frac{2.18\cdot 10^{-18}}{6.626\cdot 10^{-34}}(\frac{1}{2^2}-\frac{1}{3^2})}$ = $65.62\cdot 10^{-8}\;m$ = $656.2 nm$.
This is the red line observed (!!) in the visible spectrum of hydrogen! The other lines are also deduced from the above formula.
Bohr's theory and especially the equation (*) have played an important role in the development of wave mechanics that would apply to all atomic structures!