The Bohr atom

Detailed calculations

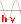
$E_{pot}$ $=$ $-\frac{ke^2}{r}\;(5) $ $E_{cin}$ $=$ $\frac{mv^2}{2}\;(6) $ $\frac{ke^2}{r^2}$ $=$ $\frac{mv^2}{r}\;(7) $ $mvr$ $=$ $\frac{nh}{2\pi}\;(8)$ where: $k$ $=$ $9\cdot 10^9\frac{Nm^2}{C^2}$ $e$ $=$ $1.6\cdot 10^{-19}C$ $m$ $=$ $9.11\cdot 10^{-31}kg$ $h$ $=$ $6.626\cdot 10^{-34}Js$ $\pi$ $=$ $3.1416$

-Eliminate $v$ between (7) and (8) in order to obtain the radius $r$ of the $n^{th}$ orbit (I)!

(8): $v$ $=$ $\frac{nh}{2\pi r m}$ $v^2$ $=$ $\frac{n^2h^2}{4\pi^2 r^2 m^2}$ in (7): $\frac{ke^2}{r^2}$ $=$ $\frac{mn^2h^2}{r4\pi^2 r^2 m^2}$ $ke^2$ $=$ $\frac{n^2h^2}{4\pi^2 r m}$ $r$ $=$ $\frac{n^2h^2}{4\pi^2 ke^2 m}\;(I)$

- Introduce into (8) in order to obtain the speed of the electron in the $n^{th}$ orbit (II)!

(8): $v$ $=$ $\frac{nh}{2\pi r m}$ (I) in (8): $v$ $=$ $\frac{nh\cdot 4pi^2ke^2m}{2\pi n^2 h^2 m}$ $v$ $=$ $\frac{2k\pi e^2}{nh}\;(II)$

- Express the total energy of the electron in the $n^{th}$ orbit as a function of $r$ (III)

$E_{tot}$=$E_{pot}+E_{cin}$ (5) and (6): $E_{tot}$ $=$ $-\frac{ke^2}{r}+\frac{mv^2}{2}$ (7): $E_{tot}$ $=$ $-\frac{ke^2}{r}+\frac{\frac{ke^2r}{r^2}}{2}$ $E_{tot}$ $=$ $-\frac{ke^2}{2r}\;(III)$

Note that the potential energy and the total energy are negative, because of the arbitrarily set zero energy at the position where the electron is located at infinite distance from the nucleus. That will not matter because the result will need only differences of energy to calculate the wavelength of the emitted photons !

- Introduce (I) into (III)

(III): $E_{tot}$ $=$ $-\frac{ke^2}{2r}$ (I) in (III): $E_{tot}$ $=$ $-\frac{ke^24\pi^2ke^2m}{2n^2h^2}$ $E_{tot}$ $=$ $-\frac{2k^2e^4\pi^2m}{n^2h^2}$

- By introducing the values of the constants given above, we finally have:

$E_{tot}$ $=$ $-2.18\cdot 10^{-18}\frac{1}{n^2}J$