Search:
These are lattices where positive ions A and negative ions B are in equal numbers.
The relative size of the ions determines the lattice type:
If positive and negative ions have approximately the same size, the lattice is often of
Cesium chloride type $(Cs^+Cl^-)$
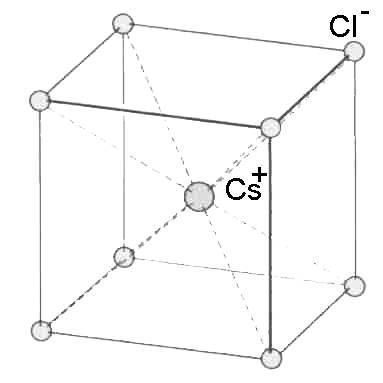If the diameter of the cations is about half the diameter of the anions, the lattice is often of
Sodium chloride type $(Na^+Cl^-)$
If the diameter of the cations is about a quarter of the diameter of the anions, the lattice is often of
Sphalerite type $(Zn^{2+}S^{2-})$
(zinc sulfide, zinc blende)
These are lattices where there are twice as many anions B than cations A.
The relative size of the ions determines the lattice type:
If positive and negative ions have approximately the same size, the lattice is often of
Fluorite type $(Ca^{2+}(F^-)_2)$
(fluorspar, calcium fluoride)
If the diameter of the cations is about half the diameter of the anions, the lattice is often of
Rutile type $(Ti^{4+}(O^{2-})_2)$
(titanium(IV) oxide)
The unit cell is the smallest structure of a lattice that repeats itself by translation through the crystal.
The cell contains $1$ cation (in the centre) and $8\cdot\frac{1}{8}$ $=$ $ 1$ anion.
The ions are in contact on the diagonal $d$ of the cell and not on an edge $a$.
Therefore:
$d$ =
diameter of the anion + diameter of the cation
$d$ $=$ $a\sqrt{3}$
Volume of the cell =
$V$ $=$ $a^3$
The cell contains $ 1$ cation (in the centre), $6\cdot\frac{1}{2}$ $=$ $3$ anions at the middle of the faces, $8\cdot \frac{1}{8}$ $=$ $1$ anion at the corners and $12\cdot \frac{1}{4}= 3$ cations at the middle of the edges. The ions are only in contact on the edge $a$ and not on the diagonal $d$. Therefore: $a$ = diameter of the anion + diameter of the cation $d$ = $a\sqrt{3}$ Volume of the cell = $V$ $=$ $a^3$
The unit cell determines often the macroscopic cristalline structure, but not always. Cristallography studies the geometry of cristals.