Konzentrationen: Molalität und Molenbruch
Lösungsmittel, gelöster Stoff und Lösung
Der gelöste Stoff ($ so $) ist die gelöste Spezies, das Lösungsmittel (sl) ist die Flüssigkeit, in der diese Spezies gelöst ist, und die Lösung (S) ist die Mischung der beiden. Die Masse der Lösung ist immer gleich der Masse des Lösungsmittels + der Masse des gelösten Stoffes.
$m_S$=$m_{so}+m_{sl}$
Eine solche Gleichheit ist für Volumes nicht immer wahr !
Molenbruch des gelösten Stoffes ($ X_{so} $)
Der Molenbruch des gelösten Stoffes ist das Verhältnis der Anzahl der Mole gelösten Stoffes zur Gesamtzahl der Mole der Mischung. Im Falle eines einzelnen gelösten Stoffes ist die Gesamtzahl der Mole der Mischung die Summe der Anzahl der Mole gelösten Stoffes und des Lösungsmittels:
$X_{so}$=$\frac{n_{so}}{n_{so}+n_{sl}}$
Molalität des gelösten Stoffes ($ \mu_{so} $)
Die Molarität des gelösten Stoffes ist das Verhältnis der Anzahl der Mole gelösten Stoffes zur Masse des Lösungsmittels.
$\mu_{so}$=$\frac{n_{so}}{m_{sl}}$
wo $m_{sl}$ in kg ausgedrückt wird
Zusammenstellung:
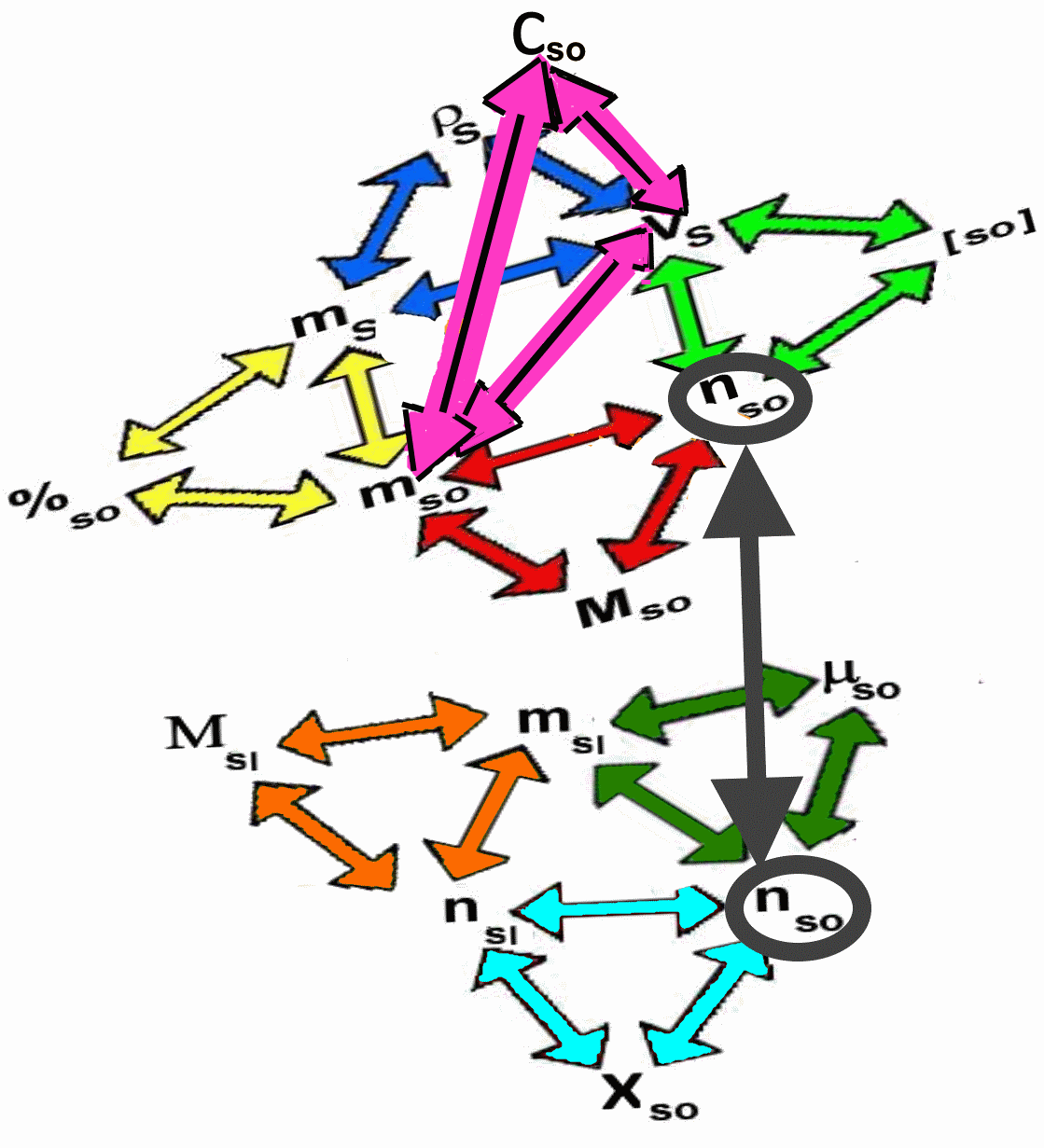
Das "Gitter"
Das folgende "Gitter" fasst die Beziehungen zwischen den vorherigen Mengen zusammen:
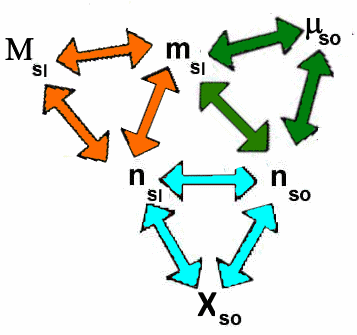
Jedes Dreieck symbolisiert eine der vorhergehenden Definitionen. Wenn wir zum Beispiel $ \mu_{so} $ und $ n_{so} $ kennen, berechnen wir $ m_{sl} $ durch das grüne Dreieck und dann $ n_{sl} $ durch das orangene Dreieck (bei Kenntnis der Molmasse) des Lösungsmittels), dann wieder $ X_{so} $ durch das blaue Dreieck!