Hier ist eine Titrationskurve, die mit einem pH-Meter aufgenommen wurde:
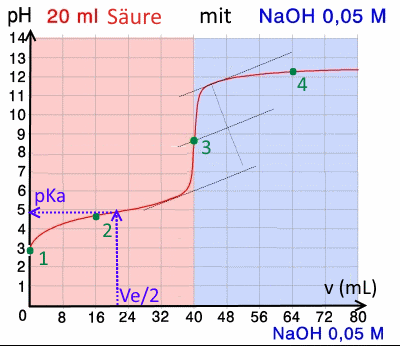
Bestimmen Sie das Volumen am Äquivalenzpunkt und berechnen Sie die anfängliche Molarität der Säure !
Für Antworten verwenden Sie die Pfeile ↑ und ↓ oben! Beenden Sie bitte diese Frage, bevor Sie zur nächsten übergehen!
$V_e$ $=$ $40\;mL$ $c_{Säure}$ $=$ $\frac{40\cdot 0,05}{20}$ $=$ $0,10M$
Bestimmen Sie die Säurekonstante !
Schwache Säure, pH am Halbäquivalenzpunkt:
$pK_a\approx 4,8$
Berechnen Sie den pH-Wert erneut auf dem Punkt 1
Schwache Säure: $x=[H_3O^+]$ $x^2+c_ax-c_aK_a$ $=$ $0$ $x^2+0,10\cdot x-0,10\cdot 10^{-4,8}$ $=$ $0$ $x=7,08\cdot 10^{-3} $ $pH$ $=$ $-log7,08\cdot 10^{-3}$ $=$ $2,15$.
Berechnen Sie den pH-Wert erneut auf dem Punkt 2
Puffer: $pH$ $=$ $4,8+log\frac{0,020\cdot 0,10-0,016\cdot 0,05}{0,016\cdot 0,05}$ $=$ $4,97$.
Berechnen Sie den pH-Wert erneut auf dem Punkt 3
Schwache Base: $x=[OH^-]$ $x^2+c_bx-c_bK_b$ $=$ $0$ $x^2+0,033\cdot x-0,033\cdot 10^{-9,2}$ $=$ $0$ $x=1,0\cdot 10^{-5} $ $pOH$ $=$ $-log[OH^-]$ $=$ $5,0$. $pH$ $=$ $14-5,0$ $=$ $9,0$.
Berechnen Sie den pH-Wert erneut auf dem Punkt 4
Starke Base im Ãœberschuss: $pH$ $=$ $14+log\frac{0,064\cdot 0,05-0,020\cdot 0,10}{0,084}$ $=$ $12,2$.
