





L'→ Aktivierungsenergie $E_a$ einer Reaktion bestimmt ihre Geschwindigkeitskonstante $k$: $k$ $=$ $Ae^{-\frac{E_a}{R\cdot T}}$
où - $T$ ist die absolute Temperatur (in $ K $) - $ E_a $ ist die Aktivierungsenergie (in $ J $) - $ R $ ist die Konstante perfekter Gase $ (8.3 \frac{J}{mol \; K}) $ - $ A $ ist ca. eine Konstante für eine bestimmte Reaktion
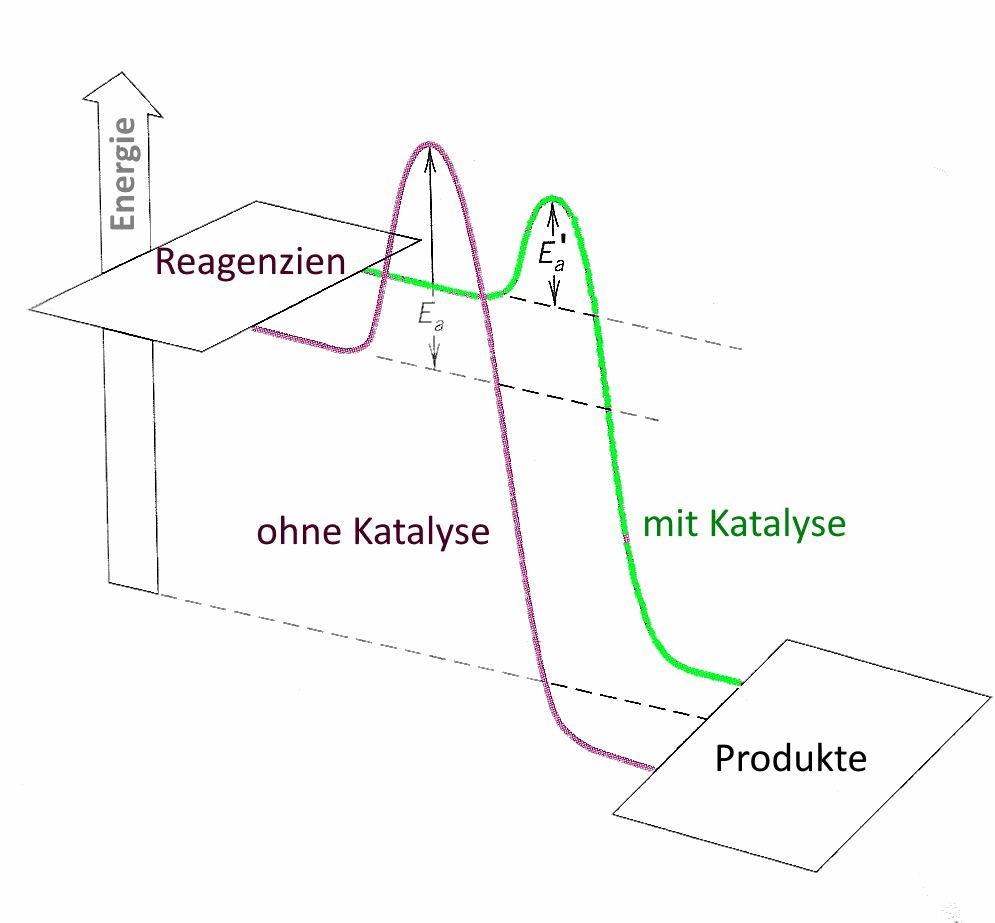
Der Katalysator verringert die Aktivierungsenergie
Wenn $ E_a $ abnimmt, steigt $ k $ und damit auch die Reaktionsgeschwindigkeit:

(1) zeigt die Entwicklung der Molarität eines Reagens $ A $ ohne, (2) mit einem Katalysator.
Angenommen, eine Reaktion hat eine Aktivierungsenergie von $ 24,9 \; kJ$ bei $ 27^oC $. Ein Katalysator senkt diese Energie auf $ \frac{1}{10} $ ihres Wertes. Berechnen Sie, um wie viel dieGeschwindigkeit erhöht wird!