





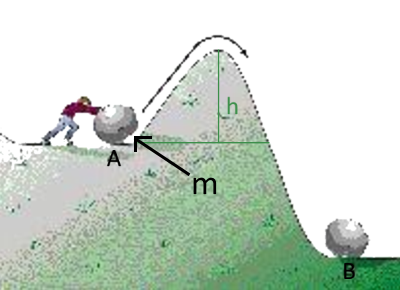
Physik Rückruf: Um den Massenball von $ A $ auf $ B $ zu drücken, muss Paul eine Arbeit verrichten von $W=9,8\;m\;h$ $m$ in $kg$ $h$ in Meter $W$ in Joule Man könnte sagen, dass diese Arbeit die Aktivierungsenergie der Transformation $ A \longrightarrow B $ ist Wenn Paul diese Energie nicht hat, kommt der Ball zurück nach $A$ !
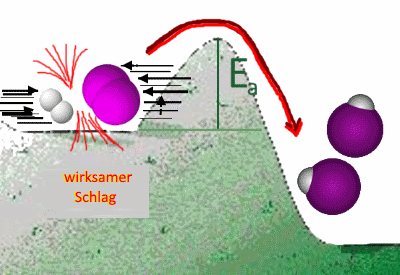
Wenn die Geschwindigkeit der Reagenzien ausreichend ist (ausreichend hohe Temperatur), werden sie in der Lage sein, die durch die Abstoßung der Atomkerne gebildete Barriere (Aktivierungsenergie) durch ihren Schlag zu überwinden und sich in Produkte umzuwandeln
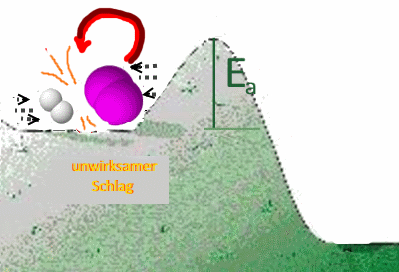
Ist die Geschwindigkeit der Reagenzien unzureichend (Temperatur nicht hoch genug) oder ist die Aktivierungsenergie zu hoch, ist dies nicht mehr möglich!

Svante Arrhénius (1859-1929)
Arrhenius stellte fest, dass die Geschwindigkeitskonstante wie folgt ausgedrückt wird:
$k=Ae^{-\frac{E_a}{R\cdot T}}$
wo - $T$ die Kelvintemperatur ist (in $K$) - $E_a$ die Aktivierungsenergie ist (in $J$ ) - $R$ die Gaskonstante ist $(8,3 \frac{J}{mol\; K} )$ - A $\approx$ eine Konstante für eine gegebene Reaktion Wir sehen, dass $ k $ (und damit die Reaktionsgeschwindigkeit) abnimmt, wenn - $ E_a $ steigt (höhere Barriere!) - $ T $ sinkt (weniger Schläge und schwächere Schläge)