Hier ist eine $ 0.050\; M $ Lösung der schwachen Base Pyridin $(C_5H_5N$ , $K_b$ $=$ $1,7\cdot 10^{-4})$
$C_5H_5N$ $ +$ $H_2O$ 
$HC_5H_5N^+$ $+$ $OH^-$
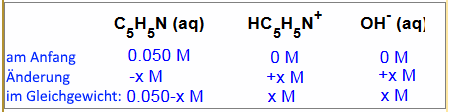
Man findet: $[OH^-]$ $=$ $x$ $=$ $1,3\cdot 10^{-2} \;M$ Wie berechnet man weiterhin den $ pH $ dieser Lösung?
a) $pH$ $=$ $- log [ H_3O^+ ]$ b) $pOH$ $=$ $- log[ OH^- ]$, dann $pH$ $=$ $14-pOH$ c) $[ H_3O^+ ]$ $=$ $\frac{K_e}{[ OH^- ]} $ , dann $pH$ $=$ $- log [ H_3O^+ ]$ d) $[ H_3O^+ ]$ $=$ $10^{-pH}$
Les voies b) ou c) sont correctes, on trouve finalement : $pH$ $=$ $12,1$