Hier ist eine $ 0.050\; M $ Lösung der schwachen Base Pyridin $(C_5H_5N$ , $K_b$ $=$ $1,7\cdot 10^{-4})$
$C_5H_5N$ $ +$ $H_2O$ 
$HC_5H_5N^+$ $+$ $OH^-$
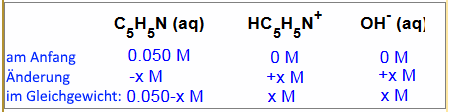
Welcher der folgenden Ausdrücke repräsentiert $K_b$ nach der Substitution?
a) $1,7 \cdot 10^{-4}$ $=$ $\frac{(0,050-x)x}{ x}$ b)$ 1,7 \cdot 10^{-4}$ $=$ $\frac{x^2 }{ 0,050}$ c) $1,7 \cdot 10^{-4}$ $=$ $\frac{0,050-x }{ x^2}$ d) $1,7 \cdot 10^{-4}$ $=$ $\frac{x^2 }{ 0,050-x}$
Antwort d) $K_b$ $=$ $1.7 \cdot 10^{-4}$ $=$ $\frac{x^2 }{ 0,050-x}$ Daher, nach Lösung der Gleichung: $[OH^-]$ $=$ $x$ $=$ $1,3\cdot 10^{-2} \;M$