



Voici une courbe de titration enregistrée au moyen d'un pH-mètre:
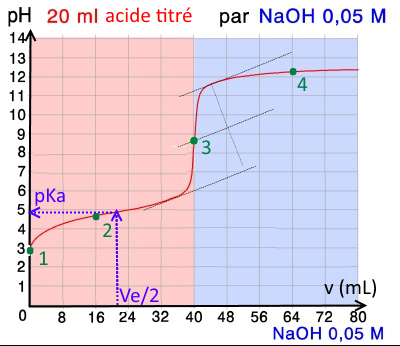
Déterminez le volume au point d'équivalence et calculez la molarité initiale de l'acide !
Pour les réponses, utilisez (éventuellement plusieurs fois) les flèches ↑ et ↓ en haut! Terminez s.v.pl. cette question avant de passer à la suivante!
$V_e$ $=$ $40\;mL$ $c_{acide}$ $=$ $\frac{40\cdot 0,05}{20}$ $=$ $0,10M$
Cherchez la constante d'acidité !
Acide faible, pH au point de demi-équivalence:

$pK_a\approx 4,8$
Recalculez le pH au point 1
Acide faible: $x=[H_3O^+]$ $x^2+c_ax-c_aK_a$ $=$ $0$ $x^2+0,10\cdot x-0,10\cdot 10^{-4,8}$ $=$ $0$ $x=7,08\cdot 10^{-3} $ $pH$ $=$ $-log7,08\cdot 10^{-3}$ $=$ $2,15$.
Recalculez le pH au point 2
Tampon: $pH$ $=$ $4,8+log\frac{0,020\cdot 0,10-0,016\cdot 0,05}{0,016\cdot 0,05}$ $=$ $4,97$.
Recalculez le pH au point 3
Base faible: $x=[OH^-]$ $x^2+c_bx-c_bK_b$ $=$ $0$ $x^2+0,033\cdot x-0,033\cdot 10^{-9,2}$ $=$ $0$ $x=1,0\cdot 10^{-5} $ $pOH$ $=$ $-log[OH^-]$ $=$ $5,0$. $pH$ $=$ $14-5,0$ $=$ $9,0$.
Recalculez le pH au point 4
Base forte en excès: $pH$ $=$ $14+log\frac{0,064\cdot 0,05-0,020\cdot 0,10}{0,084}$ $=$ $12,2$.