Loi de Maxwell-Boltzmann

Exercice 1

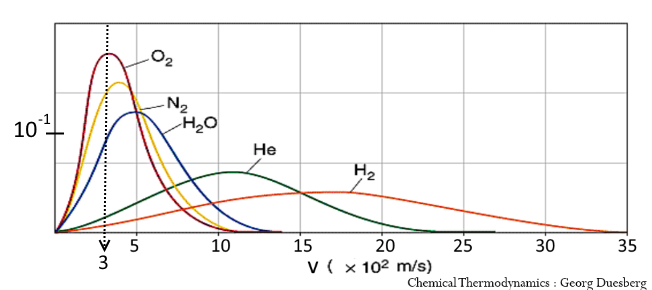
Le diagramme représente à $300\;K$ la fraction des molécules dont la vitesse se situe à $v \pm 5\frac{m}{s}$ de la vitesse donnée en abscisse. Vérifier les valeurs pour $v=300\frac{m}{s}$ en supposant que la probabilité reste constante dans cet intervalle assez petit.

$4 \pi(\frac{M}{2\pi\cdot R\cdot T})^\frac{3}{2}v^2e^{-\frac{Mv^2}{2RT} } \Delta v\,=$ $4 \cdot 3,14 (\frac{0,032}{2\cdot 3,14\cdot 8,3\cdot 300})^\frac{3}{2} 300^2 e^{-\frac{0,032\cdot 300^2}{2\cdot 8,3\cdot 300} } 10\,=$ $4 \pi(\frac{M}{2\pi\cdot R\cdot T})^\frac{3}{2}v^2e^{-\frac{Mv^2}{2RT} } \Delta v\,=$ $4 \cdot 3,14 (\frac{0,028}{2\cdot 3,14\cdot 8,3\cdot 300})^\frac{3}{2} 300^2 e^{-\frac{0,028\cdot 300^2}{2\cdot 8,3\cdot 300} } 10\,=$ $4 \pi(\frac{M}{2\pi\cdot R\cdot T})^\frac{3}{2}v^2e^{-\frac{Mv^2}{2RT} } \Delta v\,=$ $4 \cdot 3,14 (\frac{0,016}{2\cdot 3,14\cdot 8,3\cdot 300})^\frac{3}{2} 300^2 e^{-\frac{0,016\cdot 300^2}{2\cdot 8,3\cdot 300} } 10\,=$ $4 \pi(\frac{M}{2\pi\cdot R\cdot T})^\frac{3}{2}v^2e^{-\frac{Mv^2}{2RT} } \Delta v\,=$ $4 \cdot 3,14 (\frac{0,004}{2\cdot 3,14\cdot 8,3\cdot 300})^\frac{3}{2} 300^2 e^{-\frac{0,004\cdot 300^2}{2\cdot 8,3\cdot 300} } 10\,=$ $4 \pi(\frac{M}{2\pi\cdot R\cdot T})^\frac{3}{2}v^2e^{-\frac{Mv^2}{2RT} } \Delta v\,=$ $4 \cdot 3,14 (\frac{0,002}{2\cdot 3,14\cdot 8,3\cdot 300})^\frac{3}{2} 300^2 e^{-\frac{0,002\cdot 300^2}{2\cdot 8,3\cdot 300} } 10\,=$