





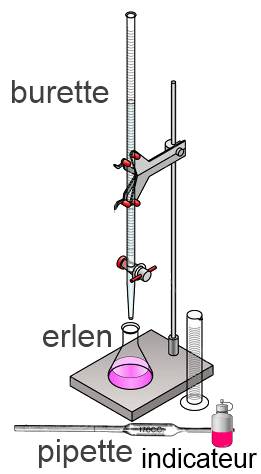
La solution à titrer est une solution dont la concentration d'un soluté 1 est à déterminer. La solution titrante est une solution dont la concentration d'un réactif 2 est connue. À l'aide d'une pipette un volume bien déterminé de la solution à titrer ( $V_1$ ) est introduit dans un erlenmeyer. On introduit quelques gouttes d'un indicateur coloré dans l'erlenmeyer. Tout en agitant l'erlenmeyer, on introduit la solution titrante jusqu'au moment où l'indicateur change (vire) de couleur. A ce moment la réaction est complète sans qu'on ait ajouté un excès de réactif. C'est le point équivalent. Sur la burette, on note le volume de la solution titrante ( $V_2$ ) écoulé.
On calcule le nombre de moles du réactif 2 consommés à l'aide de $n_2$ $=$ $[2] \cdot V_2$ ( par 2 est désigné le réactif titrant ) où $[2]$ est la concentration en moles par litre du réactif 2 À l'aide de la stoechiométrie de la réaction, on peut alors calculer le nombre de moles $n_1$ de la substance 1 dans la solution inconnue. Puis on calcule la molarité de la solution inconnue de la manière suivante: $[1]$ $=$ $\frac{n_1}{V_1}$ ( par 1 est désigné le soluté de la solution inconnue titrée )
Question
Un chimiste a trouvé un élément curieux qu'il appelle "babaorum" (symbole $Bb$). Il sait par des tests que $Bb$ est un alcalino-terreux. Son hydroxyde aura donc la formule $Bb(OH)_2$ et la réaction de ce dernier avec l'acide chlorhydrique s'écrit: $Bb(OH)_2$ $+$ $2HCl$ $\longrightarrow$ $BbCl_2$ $+$ $2H_2O$ Notre chimiste intrépide pèse soigneusement $0,257 g$ de $Bb(OH)_2$, les dissout et les titre par $HCl\; 0,2 M$. Le point équivalent est atteint après ajoute de $15 ml$ de la solution titrante. Calculez la masse atomique du babaorum!
Réponse
$n_{HCl}$=$0,2\cdot 0,015$=$0,003 mol$ Une mole $HCl$ réagit avec une demi-mole $Bb(OH)_2$: $n_{Bb(OH)_2}$ $=$ $0,0015 mol$ $M_{Bb(OH)_2}$ $=$ $\frac{m_{Bb(OH)_2}}{n_{Bb(OH)_2}}$ $=$ $\frac{0,257}{0,0015}$ $=$ $171,33\frac{g}{mol}$ $M_{Bb}$ $=$ $171,33$ $-$ $2(16+1)$ $=$ $137,33\frac{g}{mol}$