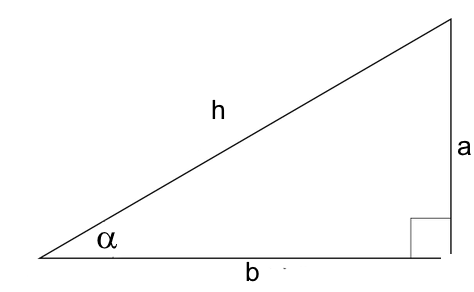
Definition im rechtwinkligem Dreieck:

   $tan\ \alpha\ =\ \frac{entgegengesetzte Seite}{angelehnte Seite}$    $tan\ \alpha\ =\ \frac{a}{b}$

Formel mit Sinus und Cosinus

   $tan\ \alpha\ =\ \frac{sin\ \alpha}{cos\ \alpha}$

   →   Beweis

    $\frac{sin\ \alpha}{cos\ \alpha}$     $=\ \frac{\frac{a}{c}}{\frac{b}{c}}$     $=\ \frac{a}{b} = tan\ \alpha$

Im trigonometrischen Kreis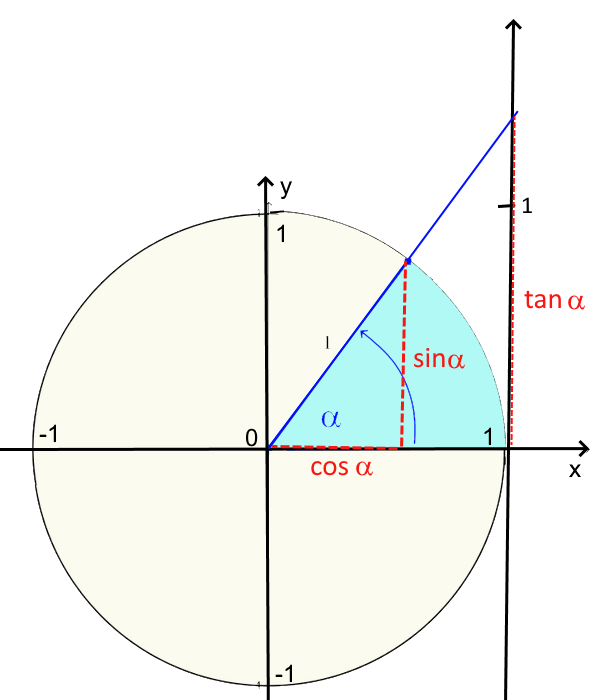

   $tan\ \alpha$ = Koordinate auf der Tangentenaxe

   →   In dedr Tat:

    Thales:     $\frac{tan\alpha}{sin\alpha}\ =\ \frac{1}{cos\alpha}$     $tan\alpha\ = \frac{sin\alpha}{cos\alpha}$ gemäß Definition

Tangente einer Summe

   $tan(\ \alpha\ +\ \beta)$ = $\frac{tan\ \alpha\ + tan\ \beta}{1-tan\ \alpha\cdot\ tan\ \beta}$

   →   EIn der Tat:

    $\frac{tan\ \alpha\ + tan\ \beta}{1\ -\ tan\ \alpha\cdot\ tan\ \beta}$     $=\frac{\frac{sin\ \alpha}{cos\ \alpha}+\frac{sin\ \beta}{cos\ \beta}}{1-\frac{sin\ \alpha}{cos\ \alpha}\ \cdot\ \frac{sin\ \beta}{cos\ \beta}}$     $=\ \frac{\frac{sin\ \alpha cos\ \beta + cos\ \alpha sin\ \beta}{cos\ \alpha cos\ \beta}}{\frac{cos\ \alpha cos\ \beta - sin\ \alpha sin\ \beta}{cos\ \alpha cos\ \beta}} $     $=\ \frac{sin\ \alpha cos\ \beta + cos\ \alpha sin\ \beta}{cos\ \alpha cos\ \beta - sin\ \alpha sin\ \beta}$     $=\ \frac{sin(\alpha\ +\ \beta)}{cos(\alpha\ +\ \beta)}$     $=\ tan(\alpha\ +\ \beta) $

Übung

   Beweise:     1)$tan(\ -\ \alpha)\ =\ -\ tan\ \alpha$     2)$tan(\pi\ -\ \alpha)\ =\ -\ tan\ \alpha$     3)$tan(\pi\ +\ \alpha)\ =\ \ tan\ \alpha$     2)$tan(\frac{\pi}{2}\ -\ \alpha)\ =\ \frac{1}{tan\ \alpha}\ =\ cotan\ \alpha $    →   ici:

    1)$tan(\ -\ \alpha)\ =\ \frac{sin( -\ \alpha)}{cos(-\ \alpha)} =\ \frac{-\ sin\ \alpha}{cos\ \alpha} =\ -\ tan\ \alpha$     2)$tan(\pi\ -\ \alpha)\ = \ \frac{sin(\pi\ -\ \alpha)}{cos(\pi\ -\ \alpha)} =\ \frac{sin\ \alpha}{-\ cos\ \alpha} =\ -\ tan\ \alpha$     3)$tan(\pi\ +\ \alpha)\ = \ \frac{sin(\pi\ +\ \alpha)}{cos(\pi\ +\ \alpha)} =\ \frac{-sin\ \alpha}{-\ cos\ \alpha} =\ \ tan\ \alpha$     2)$tan(\frac{\pi}{2}\ -\ \alpha)\ = \ \frac{sin(\frac{\pi}{2}\ -\ \alpha)}{cos(\frac{\pi}{2}\ -\ \alpha)} =\ \frac{cos\ \alpha}{sin\ \alpha} =\ \frac{1}{tan\ \alpha}\ =\ cotan\ \alpha $