
Tigonometrie
Sinussatz

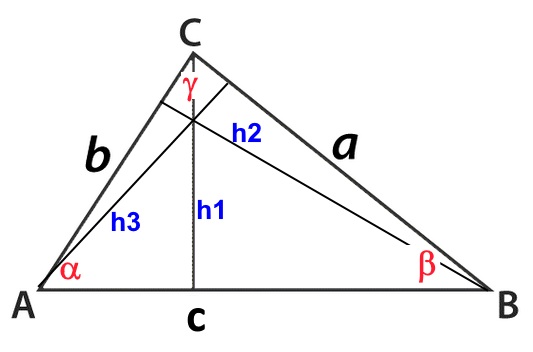
In jedem Dreieck:
$\frac{sin\alpha}{a}\ =\ \frac{sin\beta}{b}\ =\ \frac{sin\gamma}{c} $ $a$ : $\alpha$ entgegen $b$ : $\alpha$ angelehnt $c$ : $\gamma$ entgegen
Beweis
Es sei $S$ der Flächeninhalt des Dreiecks: $S\ =\ \frac{c\cdot h1}{2}\ =\ \frac{a\cdot h3}{2}\ =\ \frac{b\cdot h2}{2} $; $S\ =\ \frac{c\cdot a\cdot sin\beta}{2}\ =\ \frac{a\cdot b\cdot sin\gamma}{2}\ =\ \frac{b\cdot b\cdot sin\alpha}{2} $; Division durch $\frac{abc}{2}$ $\ \frac{c\cdot a\cdot sin\beta}{abc}\ =\ \frac{a\cdot b\cdot sin\gamma}{abc}\ =\ \frac{b\cdot b\cdot sin\alpha}{abc} $; $\ \frac{ sin\beta}{b}\ =\ \frac{sin\gamma}{c}\ =\ \frac{ sin\alpha}{a} $;
Übungen
1
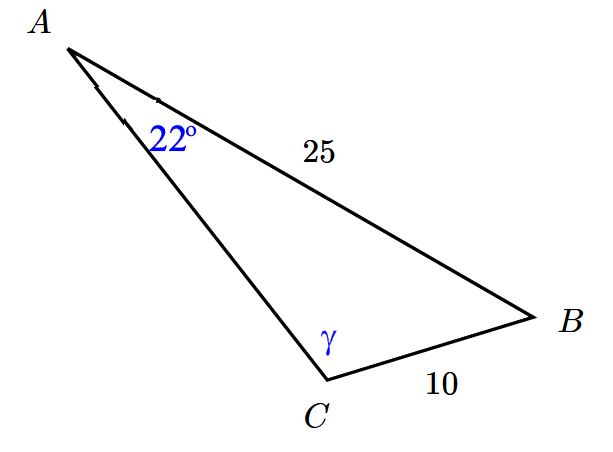 Berechnen Sie $\gamma$ !
Berechnen Sie $\gamma$ !
$\frac{sin \gamma}{25}\ =\ \frac{sin 22}{10}$ $sin \gamma\ =\ \frac{25sin 22}{10}$ $sin \gamma\ =\ 159,5^o$
2
Siehe Figur oben ! $\alpha\ =\ \frac{\pi}{6} rad$; $h\ =\ 30$ Berechnen Sie $a$!
$a\ =\ h \cdot sin\alpha\ =\ 30\cdot \frac{1}{2}\ = 15$
3
Beweisen Sie: $cos^2\alpha\ + sin^2\alpha\ =\ 1$;
$cos^2\alpha\ + sin^2\alpha\ = $ $\frac{b^2}{h^2}\ +\ \frac{a^2}{h^2}= $ $\frac{a^2+b^2}{h^2} = $ $\frac{h^2}{h^2} = 1$ (→ Pythagoras)