Poussée d'Archimède
 

     

•   Mathematiques de base
•   Physique de base
•   Chimie de base

Le principe: Force verticale

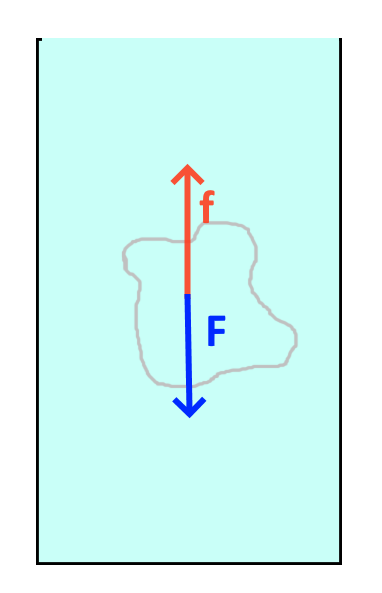
    Un corps immergé subit une poussée verticale $f$ égale au poids $F$ du liquide déplacé

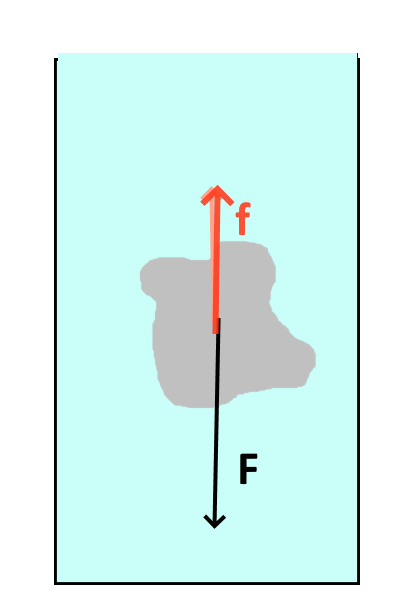
   En rempla&ccédil;ant le corps par un volume égal de liquide, on voit que ce volume restera en équilibre, donc le poids $F$ en sera égal à la poussée $f$ !

Exercices

1

    Un objet pèse $380\ N$ dans l'air , mais seulement $320\ N$ immergé dans l'eau. Volume ?    →   Calcul

   Poussée d'Archimède: $60\ N$    Poussée = Poids du même volume d'eau    $60 = 9,81\cdot V \cdot 1000 $    $V = \frac{60}{9810} = 0,0062\ m^3$

2

    Un solide pèse $45\ N$ dans l'air , mais seulement $25\ N$ immergé dans un liquide de masse volumique $800 \frac{kg}{m^3}$. $\rho_s\ ?$ ?    →   Calcul

   Pour le même volume $V$:    $m_{solide} = \rho_s\cdot V = \frac{45}{9,81}$    $m_{liquide}= 800V = \frac{45-25}{9,81}$    $\frac{ 9,81\cdot 800 \cdot V}{20}$ = $\frac{9,81\cdot V \cdot \rho_s}{45} $    $\rho_s = \frac{800\cdot 45}{20} = 1800 \frac{kg}{m^3}$    

3

 

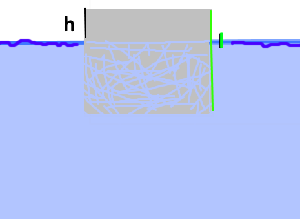
    Un morceau de glace cubique $\rho = 917\frac{kg}{m^3}; l = 2\ m$ flotte sur l'eau de mer $\rho = 1025\frac{kg}{m^3}$     Calculer $h$ !    →   Calcul

   Équilibre, donc Poids = Poussée :    $\rho_{glace} \cdot l^3 \cdot 9,81 = \rho_{eau} \cdot l^2(l-h) \cdot 9,81 $    $917 \cdot l = 1025\cdot(l - h)$    $l-h = \frac{917\cdot 2}{1025} = 1,8 m$    $h = 2-1,8 = 0,2 m$