The symmetry of molecules is essential in → stereochemistry Lattice symmetry is essential in → crystallography
Two figures are mutually symmetrical , if they can be co-ordinated by a geometric operation carried out using operators called elements of symmetry:
|
|
|
|
| Point | I | Central symmetry |
| Plan | M still designated σ | Mirror |
| Axis of rotation * | A2 still designated C2 or 2 A3 still designated C3 or 3 A4 still designated C4 or 4 A6 still designated C6 or 6 |
Rotation by 180° Rotation by 120° Rotation by 90° Rotation by 60° |
* The rotation-inversion axes are characterized by the combination of an axis and a center of symmetry. The rotation-reflection axes are characterized by the combination of an axis and a plane of symmetry.
Examples of centers of symmetry. I (sometimes designated C)
The entire frame has the center of symmetry I : A' is the image of A , B' that of B
The $ C_8H_8 $ cubane molecule has the center of symmetry I
This pyrite crystal $ FeS_2 $ has inside the center of symmetry I
Examples of symmetry planes M (still called σ)
The frog has the plane of symmetry M (still named σ) : A ' is the image of A , B' that of B , C ' that of C
The formaldehyde (methanal) molecule $ CH_2O $ has two planes of symmetry M1 (still designated σ 1) and M2 ( still designated σ 2) .
This vivianite crystal $ Fe^{2+}_3(PO_4^{3-})_2· 8H_2O $ has the plane of symmetry M (still called σ) .
Examples of axes of symmetry A2 (still designated C2 or 2)
The old amphora has four handles two to two opposite. Even though the handles are not quite right-angled, it has an axis of symmetry of order 2 A2 ( still designated C2 or 2) .
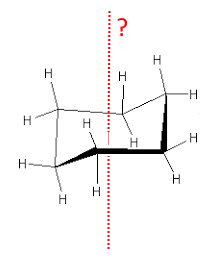
This boat conformation of 1,3-dichlorocyclohexane has an axis of symmetry of order 2 A2 ( still designated C2 or 2): All the atoms are deduced from each other by a rotation of $ 180^o $ around this axis.
The selenite $ Ca^{2+}SO_4^{2-}·2H_2O $ has a second-order symmetry axis: A2 ( still designated C2 or 2).
Examples of axes of symmetry A3 ( still designated C3 or 3)
The tetrahedron at Pen-Bron Beach has a symmetry axis of order 3: A3 ( still designated C3 or 3) . A' is the image of A .
The ammonia molecule $ NH_3 $ has a symmetry axis of order 3: A3 ( still designated C3 or 3) .
The $ SiO_2 $ quartz has a 3rd order symmetry axis: A3 ( still designated C3 or 3).
> Examples of symmetry axes A4 ( still designated C4 or 4)
The Cheops pyramid has a fourth-order axis of symmetry:
The pentaborane (9) $ B_5H_9 $ molecule has a fourth-order symmetry axis: A4 still designated C4 or 4 .
Cassiterite $ SnO_2 $ has a fourth-order symmetry axis: A4 ( still designated C4 or 4) .
Examples of axes of symmetry A6 ( still designated C6 or 6)
The old Church of Our Lady of Nazareth has a line of symmetry of order 6:
The benzene molecule $ C_6H_6 $ has an axis of symmetry of order 6: A6 ( still designated C6 or 6).
The emerald $ Be_3(Al,M)_2(SiO_3)_6, \; (M \; = \; Cr, Fe, V) $ has an axis of symmetry of order 6: A6 ( still designated C6 or 6) .
The rotation-inversion axes are characterized by the combination of an axis and a center of symmetry.
The cube has an axis of rotation-inversion of order 3:: $ \bar{A3} $ again designated $ \bar{C3} $ or $ \bar{3} $ : The point $ A $ gives by rotation of $ 120^o $ the point X (1), which, in turn, by central symmetry, gives the image point $ A'$ (2 ).
Note:
The rotation-inversion of order 1 is the composition of a 360° angle rotation and an inversion: $\bar{1}= \;i $ .
The rotation-inversion of order 2 given as an example is in fact a reflection with respect to the mirror plane perpendicular to the axis of rotation and passing through the center of inversion: $\bar{2}=\sigma $ .
The axis of rotation-reflection are characterized by the combination of an axis and a plane of symmetry perpendicular to this axis.
The tetrahedron has a rotation-reflection axis of order 4: : $S4$ : The point $A$ gives by rotation of $90^ o$ the point X (1), which, in its turn, by reflection on the plane, gives the image point $A'$ (2).
Note:
As the mirror (reflection from the plane) is equivalent to a rotation of π followed by an inversion, a rotation-reflection (by definition a rotation of θ followed by a mirror) is therefore a rotation-inversion of angle θ+π
The rotation-reflection of order 1 is therefore a mirror: $S1= \sigma $ .
The rotation-reflection of order 2 is therefore an inversion: $S2= \;i $ .
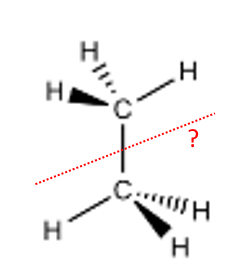
Find the vertical rotation axes (click)
Find the number of mirrors(click)
Find the number of rotation-reflection axes (click)
Click on the following figures to identify the represented element of symmetry:
