Air humidity

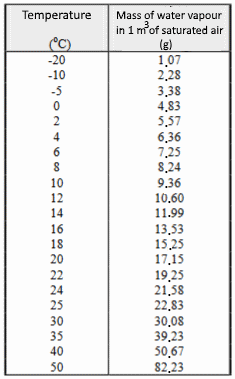
The saturated air If the water is in contact with air, agitated water molecules can enter the air. Thus invisible water vapor is mixed with gases normally present in the air. Air is said to become "humid". We feel this humidity especially in summer, in a "heavy" and stormy weather. Similarly, some water molecules forming water vapor can lose their kinetic energy by the hazards of shocks with other molecules present in the air. They join the liquid water which is in contact with the air. If this exchange continues long enough, a heterogeneous equilibrium of water is established between the "liquid water" phase and the "air" phase . The air is said to be saturated and we have: $K\;=\;\frac{[H_2O]_{air}}{[H_2O]_{eau}}$ avec: $[H_2O]_{eau}\;\approx\;55.6\frac{mol}{L}$ Indeed, 1 liter of water has a mass of about $ 1000\;g $ and thus contains about $ \frac{1000}{18}\; = \;55.6 mol $. We find thus: At equilibrium (saturated air): $[H_2O]_{air}\;=\;K_1$ Like any equilibrium constant, $ K_1 $ depends on the temperature. At higher temperatures, the molecules are more agitated and it is easy to understand that more water molecules are then in the vapor state: $ K_1 $ increases with temperature.

Example: At $ 20^oC $, the constant $ K_1 $ is equal to..........$K_1= \frac{\frac{17.5}{18}}{10^3}$ = $9.7\cdot 10^{-4}\;\frac{mol}{L}$

Unsaturated air

The saturation equilibrium often does not have time to settle and thus the concentration of water vapor in the air remains less than the concentration that the same air could contain at equilibrium. The relative humidity of the air is measured relative to the (maximum) concentration of water vapor in the saturated air. Example 1: A relative humidity of $ 35\% $ at $ 30^oC$ means that one liter of air contains ..........$\frac{35}{100}\cdot \frac{30.08}{1000}$ = $0.0105\;g$ water vapor Example 2: Air at $ 40^oC having $ 2.18 \frac{mol}{m^3} \; H_2O $ has a relative humidity of ..........$\frac{2.18\cdot 18}{50.67}\cdot 100$ = $77.4\;\%$

Condensation

If the humid and hot air cools, its water vapor concentration may soon exceed the value of $ K_1 $ ($ K_1 $ decreases with temperature). If there are nuclei of condensation (pre-existing water, dust, ions ...), the excess vapor will form liquid water around these nuclei. Example: $ 1\;m^3$ of air with $ 90 \%$ humidity cools from $ 40^oC $ to $ 10^oC $ at constant pressure. Calculate: The number of moles of water vapor at the beginning: ..........$\frac{90}{100}\cdot \frac{50.67}{18}$ = $2.53\;mol$ The final volume (Gay-Lussac law): ..........$V\;=\; \frac{1\cdot 283.15}{\;313.15}$ = $0.904\;m^3$ The number of moles that the final volume can contain maximum: ..........$0.904 \cdot \frac{9.36}{18}$ = $0.470\;mol$ The number of moles and the condensed water mass: ..........$n$ = $2.53-0.47=2.06\;mol$
$m=n\;cdot M=2.06\cdot 18=37.0\;g$

Clouds, rain, fog, mist

Wet air masses that cool (upward air in a low-pressure area or on the slopes of a mountain range, less dense warm air raised above more dense cold air in a disturbance, humid air cooling by radiation during the clear nights of autumn, humid kitchen air touching the cold glass ..) can lose water vapor by condensation, if their relative humidity was sufficient from the beginning: Clouds, mists or fogs form. One can count $ 1^oC$ of cooling per $ 100\;m $ of vertical distance if there is no condensation, $ 0.5^oC $ per $ 100\;m $ in case of condensation (exothermic phenomenon).

.

Upward air forms cumulus clouds

2