



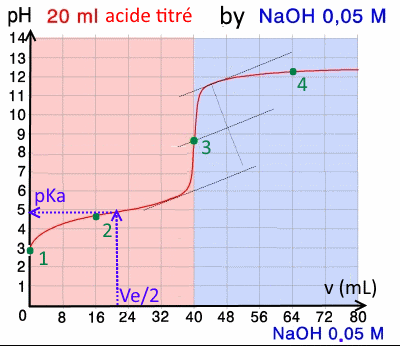
Here is a titration curve recorded using a pH meter::

Determine the volume at the equivalence point and calculate the initial molarity of the acid !
For answers, use (possibly several times) the arrows ↑ Down! and ↓ Up! Complete please this question before moving on to the next one!
$V_e$ $=$ $40\;mL$ $c_{acide}$ $=$ $\frac{40\cdot 0.05}{20}$ $=$ $0.10M$
Look for the acidity constant !
Weak acid, pH at half-equivalence point:
$pK_a\approx 4.8$
Recalculate the pH at point 1
Weak acid: $x=[H_3O^+]$ $x^2+c_ax-c_aK_a$ $=$ $0$ $x^2+0.10\cdot x-0,10\cdot 10^{-4.8}$ $=$ $0$ $x=7,08\cdot 10^{-3} $ $pH$ $=$ $-log7.08\cdot 10^{-3}$ $=$ $2.15$.
Recalculate the pH at point 2
Buffer: $pH$ $=$ $4.8+log\frac{0.020\cdot 0.10-0.016\cdot 0.05}{0.016\cdot 0.05}$ $=$ $4.97$.
Recalculate the pH at point 3
Weak base: $x=[OH^-]$ $x^2+c_bx-c_bK_b$ $=$ $0$ $x^2+0.033\cdot x-0.033\cdot 10^{-9.2}$ $=$ $0$ $x=1.0\cdot 10^{-5} $ $pOH$ $=$ $-log[OH^-]$ $=$ $5.0$. $pH$ $=$ $14-5.0$ $=$ $9.0$.
Recalculate the pH at point 4
Excess strong base: $pH$ $=$ $14+log\frac{0.064\cdot 0.05-0.020\cdot 0.10}{0.084}$ $=$ $12.2$.