Acid-base titration
Tutorial 20
pH during titration of a weak base by a strong acid
Schematic:
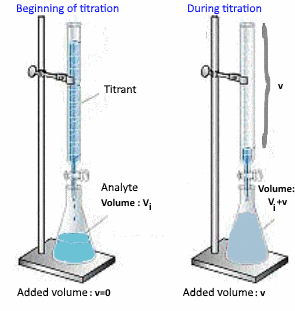
Determining the acid volume $ V_e $ added at the equivalent point
$ n_{added \;acid } = n_{initial \; base} $
$ V_e \cdot c_{acid} = V_i \cdot c_{base} $
Hence $ V_e $
pH by volume $ v $ of base added
$ v = 0 $
pH of a weak base of molarity $ c_{base} $:
$ x = [OH^-] $
$ x ^ 2 + c_{base} x-c_{base} K_a = 0 $
etc...
$v\lt V_e$
Determine the numbers of weak base moles $ n_b $ that have not yet reacted as well as the number of moles of weak acid $ n_b $ formed.
pH of buffer !
$pH=pK_a+log\frac{n_b}{n_a}$
$v=V_e$
pH of a weak acid $c_a$:
The number of moles of weak acid present at this time $n_a$ $=$ $n_{added \; acid}$ $=$ $ n_{initial\;base}$
Then: $c_a=\frac{n_a}{V_i+V_e}$
and with
$x=[H_3O^+$:
$x^2+c_ax-c_aK_a=0$
etc..
$v\gt V_e$
Determine the numbers of moles of strong acid $ n_a $ in excess
$pH=-log\frac{n_a}{V_i+v} $
$ 20 \; mL $ ammonia $ NH_3 $ are titrated by $ HCl \; 0.1 \; M $. At the equivalent point, $ 25 \; mL \; HCl $ have been added so far.
Calculate the initial molarity of $NH_3 $
For answers, use (possibly several times) the arrows ↑ Down! and ↓ Up!
Complete please this question before moving on to the next one!
$V_e\cdot c_{acide}=V_i\cdot c_{base}$
$0.025\cdot 0.1$ $=$ $0.020\cdot c_{NH_3}$
$c_{NH_3}$ $=$ $0.125\;\frac{mol}{L}$
