Maxwell-Boltzmann law:

Exercise 1

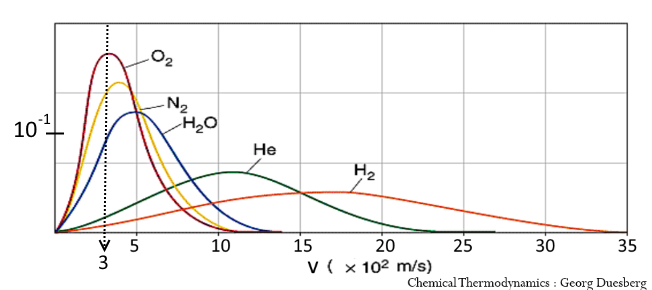
The diagram represents at $300\; K$ the fraction of molecules whose speed $v$ is in the interval $ \pm 5 \frac{m}{s} $ from the speed given on the abscissa. Check the values for $ v = 300 \frac{m}{s}$ assuming that the probability remains constant in this relatively small range.

$4 \pi(\frac{M}{2\pi\cdot R\cdot T})^\frac{3}{2}v^2e^{-\frac{Mv^2}{2RT} } \Delta v\,=$ $4 \cdot 3.14 (\frac{0.032}{2\cdot 3.14\cdot 8.3\cdot 300})^\frac{3}{2} 300^2 e^{-\frac{0.032\cdot 300^2}{2\cdot 8.3\cdot 300} } 10\,=$ $4 \pi(\frac{M}{2\pi\cdot R\cdot T})^\frac{3}{2}v^2e^{-\frac{Mv^2}{2RT} } \Delta v\,=$ $4 \cdot 3.14 (\frac{0.028}{2\cdot 3.14\cdot 8.3\cdot 300})^\frac{3}{2} 300^2 e^{-\frac{0.028\cdot 300^2}{2\cdot 8.3\cdot 300} } 10\,=$ $4 \pi(\frac{M}{2\pi\cdot R\cdot T})^\frac{3}{2}v^2e^{-\frac{Mv^2}{2RT} } \Delta v\,=$ $4 \cdot 3.14 (\frac{0.016}{2\cdot 3.14\cdot 8.3\cdot 300})^\frac{3}{2} 300^2 e^{-\frac{0.016\cdot 300^2}{2\cdot 8.3\cdot 300} } 10\,=$ $4 \pi(\frac{M}{2\pi\cdot R\cdot T})^\frac{3}{2}v^2e^{-\frac{Mv^2}{2RT} } \Delta v\,=$ $4 \cdot 3.14 (\frac{0.004}{2\cdot 3.14\cdot 8.3\cdot 300})^\frac{3}{2} 300^2 e^{-\frac{0.004\cdot 300^2}{2\cdot 8.3\cdot 300} } 10\,=$ $4 \pi(\frac{M}{2\pi\cdot R\cdot T})^\frac{3}{2}v^2e^{-\frac{Mv^2}{2RT} } \Delta v\,=$ $4 \cdot 3.14 (\frac{0.002}{2\cdot 3.14\cdot 8.3\cdot 300})^\frac{3}{2} 300^2 e^{-\frac{0.002\cdot 300^2}{2\cdot 8.3\cdot 300} } 10\,=$