





Definition Is called momentum $p$ of a body the product of its mass and velocity:
Momentum: $p$ $=$ $m\cdot \vec{v}$ where: $m$ is mass $\vec{v}$ is velocity
The fundamental law Use one of the → initial assumptions of the kinetic theory of gases: $\vec{F}=m\frac{\Delta \vec{v}}{\Delta t}$ $\vec{F}=\frac{\Delta m\vec{v}}{\Delta t}$
Force: $\vec{F}=\frac{\Delta \vec{p}}{\Delta t}$ The force is equal to the variation of the momentum

If the shock is elastic, the molecule having a velocity $\vec{V}\binom{v_x}{v_y}$ rebounds with a velocity $\vec{Vī}\binom{-v_x}{v_y}$ The variation of the momentum is then: $\Delta{p}$ = $\Delta m\vec{v}$ = $m\binom{-v_x}{v_y}-m\binom{v_x}{v_y}$ = $m\binom{-2v_x}{0}$

Our ideal gas consists of molecules that move without interacting randomly in all directions in a box of volume $V = A\cdot L$ Proceed by steps to find the pressure on the wall $A$:
Consider one molecule: - Its speed in the direction $x$ is $v_x$ before or after its impact against the wall $A$ - The time between two shocks against the same wall is the time to make a return trip in the box in the direction $x$

- Using formula: time = $\frac{distance}{velocity}$ this time can be evaluated by: $\Delta t=\frac{2L}{v_x}$ The intensity of the force exerted by the wall on the molecule is therefore $f =$ $\frac{1}{\Delta t}2mv_x =$ $\frac{2mv_x}{\frac{2L}{v_x}} =$ $\frac{mv_x^2}{L}$ According to Newton's law of action and reaction this is also the intensity of force that the molecule had exerted on the wall!
Consider all molecules $1,2,3,4,5,..........N$ of the box. Then the force exerted on the wall $A$ is $F=$ $f_1+f_2+f_3+f_4+f_5+......f_N =$ $\frac{m[v_{1x}^2+v_{2x}^2+v_{3x}^2+v_{4x}^2+v_{5x}^2+......v_{Nx}^2]}{L}$ Let's call $u_x^2$ the average of the squares of the components of the velocity in the direction x, $u_y^2$ the average of the squares of the components of the velocity in the direction y, $u_z^2$ the average of the squares of the components of the velocity in the direction z, $u^2$ the average of the squares of the real velocities so: $u_x^2 =$ $\frac{m[v_{1x}^2+v_{2x}^2+v_{3x}^2+v_{4x}^2+v_{5x}^2+......v_{Nx}^2]}{N}$ and then: $F=$ $\frac{mNu_x^2}{L}$ As we have assumed that there is no privileged direction to the movement of molecules in the gas, we can say that $u_x^2=u_y^2=u_z^2$
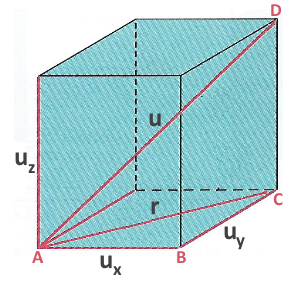
Use the Pythagorean theorem for triangles ABC and ACD: $r^2$ $=$ $u_x^2+u_y^2$ $u^2$ $=$ $r^2+u_z^2$ $=$ $u_x^2+u_y^2+u_z^2=3u_x^2$ then: $F=$ $\frac{mNu^2}{3L}$
Using the definition of pressure: $P$ = $\frac{F}{A}$ we find $P$ = $\frac{\frac{mNu^2}{3L}}{A} =$ $\frac{mNu^2}{3L\cdot A} =$ $\frac{mNu^2}{3V}$
Pressure of the gas $P=\frac{mNu^2}{3V}$ where $V$ is the volume of the gas $m$ is the mass of one molecule $N$ is the number of molecules