





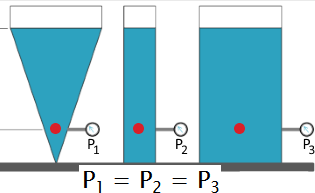
In a water point pressure exerts in all directions:
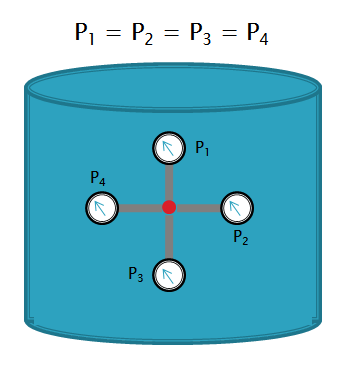
This pressure is the sum of two pressures: - The surface atmospheric pressure - The pressure exerted by the water which solely depends on the depth
The pressure of the water is given by: $P_ {water}$ $= $ $\rho_ {water} \cdot g \cdot h$ where $P_{water} $is expressed in Pascal $(1\;Pa$ $=$ $10^{- 5}\;bar$\approx $10^{-5}\;atm) $ $\rho_{water} = 1000\frac{kg}{m^3} $is the mass density of water $g \approx 10 \frac{Pa\cdot m^2}{kg} $ $h$ is the depth of water, expressed in $m$
Example The pressure exerted by water at $10\;m$ depth is: $P_{water} $ $= $ $1000\cdot 10 \cdot 10 \approx 10^5 Pa $ $= $ $\;bar$ $\approx$ $1\;atm$ In the sea, where there is a pressure of $1\;bar$ on surface, the pressure at $10\;m$depth is therefore $1 + 1 = 2 \;bar $ Practical rule
In the water pressure increases by $1\;bar\approx 1\; atm $ all $10\;m$
Exercise A diver stays at 25m depth long enough for equilibrium to be established between the air he breathes at ambient pressure and blood. Then calculate the molarity of the nitrogen in the blood (which we assimilate here with water)
Definition In general, the dives are quite brief so that the equilibrium between nitrogen and nitrogen breathed a given tissue has no time to settle. To every molarity of nitrogen less than the molarity at equilibrium there is a corresponding pressure according to Henry's Law. This is the pressure at which the plunger is exposed from Henry's law if he were already equilibrated with the molarity in question. It is called nitrogen "tension".
The nitrogen tension of a tissue is the equilibrium pressure corresponding to the instantaneous concentration of nitrogen in a given tissue of the diver
Example A diver descended rapidly to $10\;m$. The nitrogen pressure in one of its tissues is $1.3\; atm$: Then the molarity of the nitrogen in this tissue is $[N_2] $ $= $ $6.1 \cdot 10^{-4} \cdot 1.3 $ $= $ $7.9 \cdot 10^{-4} \frac{mol}{L} $ He remains long enough at this depth so that equilibrium is established: Then the molarity of the nitrogen in this tissue is $[N_2]$ $= $ $6.1 \cdot 10^{-4} \cdot 2.0 $ $= $ $1.2 \cdot 10^{-3} \frac{mol}{L} $ Period of a tissue For a first diver down very quickly from the surface of the sea to a depth of $10\; m$, there must be $5 $ minutes for blood to achieve a nitrogen pressure of $1 + \frac{2-1}{2} $ $= $ $1.5 \; atm ,$ ie to dissolve one half of the maximum amount permitted to this depth. For a second diver down very quickly from the surface of the sea to a depth of $20\; m $, there must be $5 $ minutes for blood to reach a nitrogen pressure of $1 + \frac{3-1}{2} $ $= $ $2.0 \; atm ,$ ie to dissolve one half of the maximum amount permitted to this depth. If the first diver descends quickly now to a depth of $20\;m$, there must also be $5$ minutes for his blood to achieve a nitrogen pressure of $1.5 + \frac{3-1.5}{2} = 2.25\;atm,$ ie to dissolve half the maximum amount permitted to this depth. If the second diver goes now back quickly to a depth of $10\; m $, there must also be $5$ minutes for his blood to achieve a nitrogen pressure of $2,25 - \frac{2,25-2,0}{2}=2,125\; atm,$ ie to dissolve one half of the maximum amount permitted to this depth. It is said that the period of the tissue blood is $5$ minutes!
The period of a tissue is - the time required to dissolve (or eliminate) at a given depth half the amount of nitrogen which remains to dissolve (or eliminate) - for a given depth, the time needed to reach the mean tension between the instantaneous tension and the pressure at equilibrium
After a deep dive, a diver ascends to a shallower depth where he remains to make a "decompression stop" Here the nitrogen tension decay curve of one of its tissue nitrogen tensions at the depth and temperature of the decompression stop starting from an initial value to the pressure (tension) at equilibrium. Note that half of the half is a quarter, half of a quarter an eighth etc ..
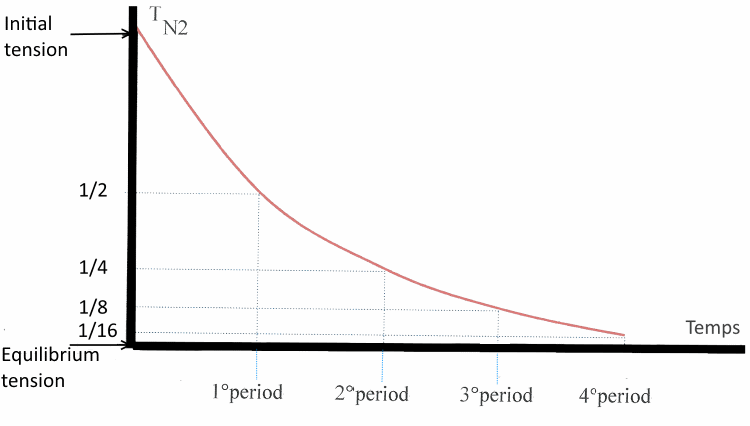
This curve predicts the nitrogen tension depending on the time spent at the decompression stop, the accumulated tension during deep depth diving, the depth of the decompression stop and the period of the corresponding tissue: Mathematical approach: This is a decreasing exponential function as we know for radioactivity or for first order kinetics of chemical reactions: $ln\frac{T-T_o}{T_i-T_o}$ $=$ $-kt$ $T-T_o$ $=$ $(T_i-T_o)e^{-kt}$ where $T$is the time stayed at the decompression stop $T_i$is the accumulated nitrogen tension during deep sea diving $T_o$is the equilibrium nitrogen tension at the decompression stop $T$is the nitrogen tension of the tissue after time $t$at the decompression stop Note that for $t = t_{\frac{1}{2}} = $period, we have $T-T_o=\frac{T_i-T_o}{2}$which gives: $ln2=\frac{k}{t_{\frac{1}{2}}}$ Nothing prevents to use that as above in case of a diver who goes down to a given depth and stays for a given time!
For a given tissue: $T $ $= $ $T_o + (T_i-T_o) e^{- kt} $ where $T $is the time stayed at a given depth $T_i $is the accumulated nitrogen tension before the stay at that depth T_o $ $is the equilibrium nitrogen tension at that depth $T $is the nitrogen tension after the residence time $t$at that depth $k=\frac{ln2}{t_{\frac{1}{2}}}$ $t_{\frac{1}{2}}$ is the period of the tissue or simplifying: $T$ $=$ $T_o+(T_i-T_o)2^{-\frac{t}{t_{\frac{1}{2}}}}$
Example: Determine the nitrogen tension: Dive from the surface of the sea to $40\;m$ Duration: $30$ minutes Period Fabric: $10$ minutes: $T_o = 0.8 \ cdot 5 = 4 \; $atm $T_o=0,8\cdot 5= 4\;atm$ $T$ $=$ $4+(0,8-4)e^{-\frac{ln2}{10}30}\approx 3,6\;atm$
Simplified method $e^{-\frac{ln2}{10}30}=e^{ln2\cdot{-\frac{30}{10}}}=2^{-\frac{30}{10}}=2^{-3}=\frac{1}{8}$ So: $T$ $=$ $T_o+(T_i-T_o)Q$ with $Q=\frac{1}{2}$ for $t=t_{\frac{1}{2}}$ $Q=\frac{1}{4}$ for $t=2t_{\frac{1}{2}}$ $Q=\frac{1}{8}$ for $t=3t_{\frac{1}{2}}$ etc.. Example: Determine the nitrogen tension: Updive to a level of $9\;m$ with a nitrogen tension $T = 3.6\; atm$ Time on decompression stop: $20$minutes Tissue of period: $5$ minutes: $T_o$ $=$ $0,8\cdot 1,9$ $= $ $1,52\;atm$ $T$ $=$ $1,52+(3,6-1,52)\frac{1}{16}$ $\approx $ $1,65\;atm$
Compartments
All tissues of the human body that have the same time form a compartment
In (french) diving theory, it is currently worked with $12$compartments: - The "fast" has a period of $5$ minutes. It contains the blood. - The "slow" has a period of $120$ minutes. It contains the adipose tissue.
The critical supersaturation

The gas bubbles in the water are formed as soon as the bottle is opened because the tension value of carbon dioxide in water is so much higher than the partial pressure time of this gas in the air. Which is the cause of the supersaturation and the appearance of bubbles. In the tissues of the human body the appearance of nitrogen bubbles causes decompression sickness that divers must avoid at all costs: It was determined for each of the $12$ compartments a limit ratio called coefficient of critical supersaturation:
Coefficient of critical supersaturation: $S_C = \frac{T}{P} $ where $T $is the tension of nitrogen which does not be exceeded under risk of bubble formation in this tissue $P$is the absolute pressure at the considered depth
| Period (min) | $S_c$ |
|---|---|
| 5 | 2.72 |
| 7 | 2.54 |
| 10 | 2.38 |
| 15 | 2.20 |
| 20 | 2.04 |
| 30 | 1.82 |
| 40 | 1.68 |
| 50 | 1.61 |
| 60 | 1.58 |
| 80 | 1.56 |
| 100 | 1.55 |
| 120 | 1.54 |
Example: Calculate the nitrogen tension not to be exceeded to avoid oversaturation in the compartment $10`$ a) at a depth of $6,5\;m$ in the sea. b) at a depth of $8\;m$ in the sea. a) $S_c=\frac{T}{T_o}$ $T$ $=$ $S_c\cdot T_o$ $=$ $2.38\cdot 1.65$ $=$ $3.92\;atm$ a) $S_c=\frac{T}{T_o}$ $T$ $=$ $S_c\cdot T_o$ $=$ $2.38\cdot 1.80$ $=$ $4.28\;atm$ This means that a diver having a tension $T $ $= $ $4.0\;atm$ in its $10` $ compartment risks decompression sickness at $6.5\;m $, but not at $8.0\;m $
The decompression stops
Classical decompression stops are at $9\;m$ $6\;m$ $3\;m$ (French standard, not the same in other countries!)
Usually one chooses a deep enough decompression stop so that the absolute pressure will be such that the diver does not risk decompression sickness for all its compartments.
Example: When diving into the sea to a depth of $30\;m$ for $20$ minutes, we consider two compartments: $10`$ and $20`$ a) Calculate the nitrogen tension at the end of the dive for each compartment b) What is the leading tissue and at what classical depth will it have to make a decompression stop (assuming that these are the only two compartments, which is not the case!) c) In case of decompression stop, what is the minimum duration of this?