





If the vapour of a substance occupies a given space, it has at equilibrium only one vapour pressure, regardless of the source of its molecules.
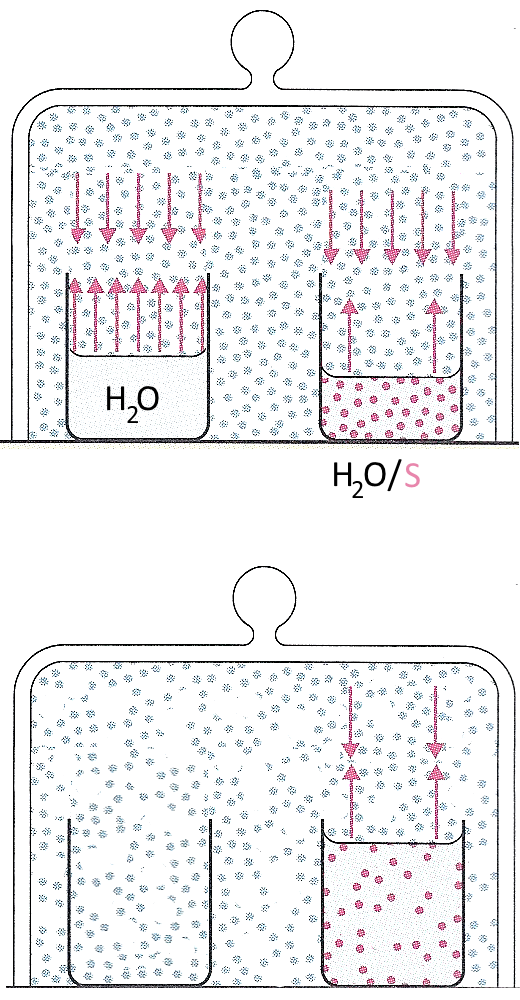
Let be - $P$the saturation vapour pressure of pure water at the temperature of the experiment. - $P$the saturation vapour pressure of water above the aqueous solution of sugar $S$ We have: $p = X_ {H_2O} \cdot P$ (Raoult's Law, sugar is non-volatile) with: $X_ {H_2O} $ molar fraction of water in the solution $X_{H_2O}=\frac{n_{H_2O}}{n_{H_2O}+n_S}\lt 1$ so: $p\lt P$ Pure water releases vapour at a pressure above the saturation vapor pressure of the water/sugar solution. As there can be only one saturation vapour pressure of the substance, the solution will try to reduce this pressure by capturing molecules released by pure water, and this as long as there is the pure water in presence. That explains is the transfer of all the water to the solution!
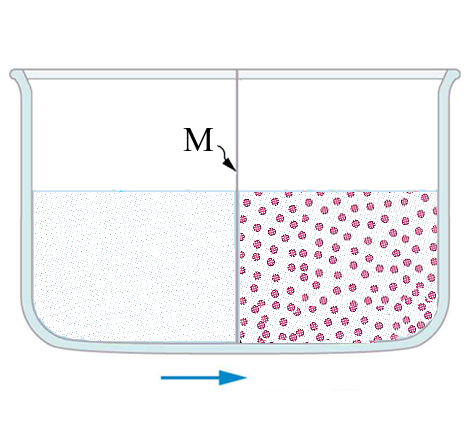
$M$ is a semi-permeable membrane. It lets the water molecules through, but not those of sugar that are larger. We can compare this membrane $M$ to the vapour phase in the previous experiment which explains the transfer of water molecules to the sugar solution:
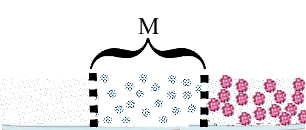
Gradually, as the volume of the sugar solution increases, it is under increasing additional hydrostatic pressure:

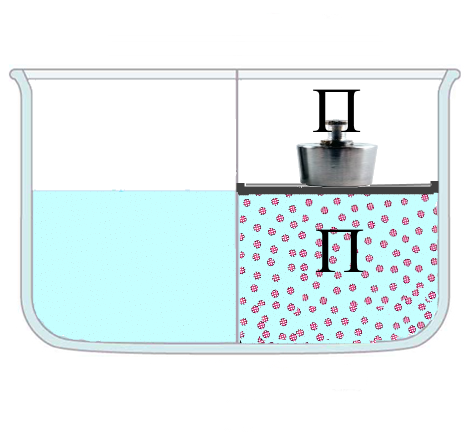
$\Pi = \rho \cdot g \cdot h$ (see Physics) where $\rho $ is the mass density $g$ is the acceleration of gravity This pressure causes the water molecules of the sugar solution to pass more frequently through the membrane and there comes a point where the transfer rates are the same in both directions. From that moment on the height $h$ does not change any more and pressure $\pi$ is called osmotic pressure.
The osmotic pressure of an aqueous solution is defined as the minimum pressure that must be applied to prevent the passage of water through the solution of a semi-permeable membrane

Jacobus Henricus van't Hoff (1852-1911)
Van't Hoff had the brilliant intuition to consider that the solute molecules in a solution behave like a gas irrespective of the solvent! We can (try to) justify his intuition as follows: - If you exert artificially a pressure equal to $\pi$ on the previous experience solution you maintain an equal level of water and solution. That´s why at that point the solution (solvent water and solute) must exert a pressure equal to $\pi $, but in reverse:
- If the solute is removed, there is no need to exert an external pressure or an opposite pressure to maintain the level. Water is not responsible for $\pi $
- Therefore it is the only solute which exerts the pressure $\pi$. Or look at the model:
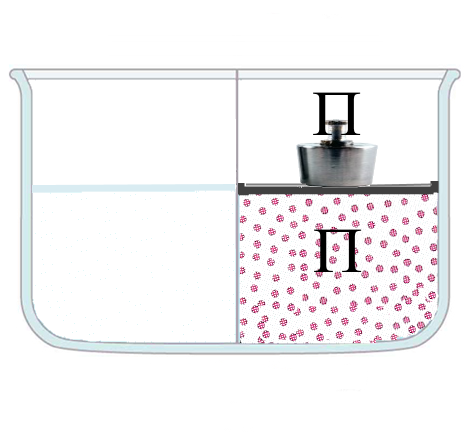
- This is indeed the model of an ideal gas, which everyone knows, and which exerts pressure: $\pi = \frac{n}{V} RT$
Van't Hoff´s law: The osmotic pressure of an aqueous solution of a solute $S$in any solvent is: $\Pi= [S]RT$ where $[S]$ is the molarity of the solute $R=0.082\frac{l\cdot atm}{mol\cdot K}=8.3\frac{J}{mol\cdot K}$ the ideal gas constant $T=t^o C+273.15$ the Kelvin temperature ($K)$
Calculate the osmotic pressure of a sucrose $0.1\;M$ solution at $27^oC$
Hitherto has been considered the case of a solution separated of the pure solvent by the semipermeable membrane. The above reasoning is valid in the case of two solutions of different concentrations. It is sufficient to consider one of the solutions "entirely" as a solute and therefore the reasoning will apply only to the difference between the molarities. $\Pi= \Delta[S]RT$ where $\Pi$ is the osmotic pressure of the most concentrated solution.
Calculate the difference between the concentrations of solutes $S$ on either side of a semipermeable membrane causing an osmotic pressure of $5\;atm$at $37\;^oC$
An ionic substance releases by "molecule" 2,3 or more ions and it is they who determine the osmotic pressure. Van't Hoff´s law applied on a sodium fluoride solution (2 ions released) should give for example $\pi = 2 [NaF]RT $ In fact a fraction of the ions are not dissociated in the solution such that the effective number of particles is still less than 2: $\pi = i [NaF] RT $ with $1\lt i \lt 2$ If $n$ is the number of ions that can be produced and $\alpha$ is the degree of dissociation (The ratio of the number of "molecules" dissociated and the number of "molecules" present before dissociation) then: For a "molecule" initially present, it will remain $1- \alpha $ "molecules" undissociated and there will be produced $n \alpha $ ions. So we will have in all: $i$ $=$ $1-\alpha+n\alpha$ $=$ $1+\alpha(n-1)$ particles!
Van't Hoff´s law: The osmotic pressure of an aqueous solution of an ionic solute $S$ soluble in a given solvent is: $\pi = i [S] RT$ $i = 1 + \alpha (n-1) $ (Van't Hoff factor) where $[S]$ is the molarity of the solute $R=0.082\frac{l\cdot atm}{mol\cdot K}=8.3\frac{J}{mol\cdot K}$ the ideal gas constant $T=t^o C+273.15$ the Kelvin temperature $K$ $\alpha $ the degree of dissociation (= $\frac{number\; dissociated}{total\;number }) $ $n$ the number of ions
Calculate the osmotic pressure of a $0.1\;M$ sodium sulfate solution at $27^oC$ $(\alpha \approx 0.7)$
Exercises To try → here