A liquid mixture of molecules $A$ and $B$ is ideal if $A-B$ attractions are as strong as $A-A$ or $B-B$

François Marie Raoult (1830-1901)
Example
Suppose we have an ideal liquid mixture of one mole of $A$ and three moles of $B$ in a closed vessel. Then the molecules of $A$ occupy only the surface of the mixture in the proportion of $\frac{1}{4}.$ When the equilibrium between liquid and gas is reached, the molecules of $A$ exchanged per unit of time between liquid phase and gas phase are only $\frac{1}{4}$ of what they would be if $A$ was alone in the liquid phase, so the partial pressure of $A$ in the gas phase at equilibrium is only $\frac{1}{4}$ of its saturation vapour pressure! The molecules of $B$ occupy also the surface in proportion to $\frac{3}{4}$, the partial pressure of $B$ in equilibrium in the gas phase is $\frac{3}{4 }$ of its saturation vapour pressure! The total pressure of the gaseous phase is obviously equal to the sum of these two partial pressures (Dalton's law)
General
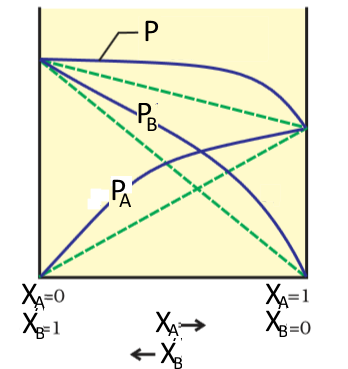
The partial pressures in a gas phase in equilibrium with an ideal mixture of two liquids are: $ P_A=X_A\; P_{oA} $ $ P_b=X_B\; P_{oB} $ The total pressure of the gas phase in equilibrium with an ideal mixture of two liquids is: $P=X_A\; P_{oA}+X_B\; P_{oB}$ where $X_A$ is the molar fraction of $A$ in the liquid phase $X_B$ is the molar fraction of $B$ in the liquid phase $P_{oA}$ is the saturation vapor pressure of $A$ $P_{oB} $ is the saturation vapor pressure of $B$
Illustration
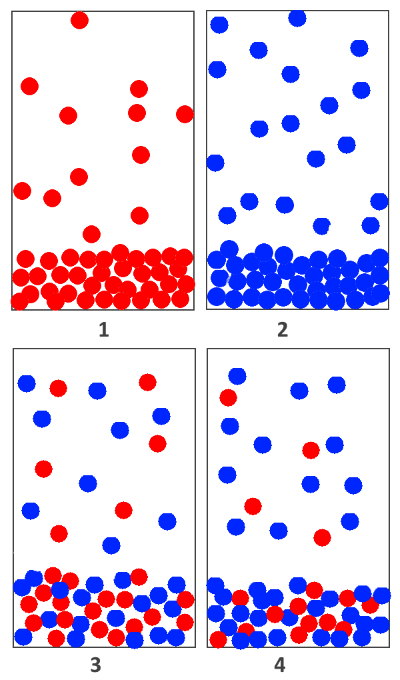
Equilibria in a closed vessel: 1: Substance $A$ liquid and vapour 2: Substance $B$ liquid and vapour 3: $X_A$ $=$ $\frac{1}{2}$ and $X_B$ $=$ $\frac{1}{2}$ 4: $X_A$ $=$ $\frac{1}{3}$ and $X_B$ $=$ $\frac{2}{3}$ Count molecules 3 and 4 in the gas phase and compare with 1 and 2!
Diagrams
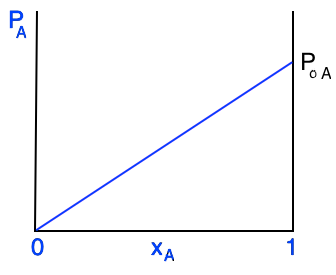
Vapour pressure diagram of $A$ as a function of its mole fraction in the liquid phase
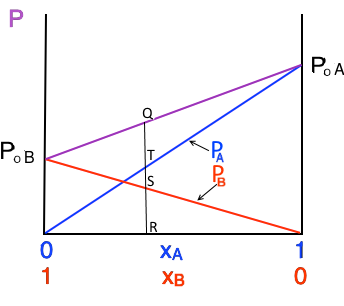
Vapour pressure diagram of $A$, $B$ and the total pressure. Note that $RQ = RS + RT$ (Dalton)
Using the ideal gas law for the gas phase: $n_A$ $=$ $\frac{P_A\;V}{RT}$ $n_B$ $=$ $\frac{P_B\;V}{RT}$ $n_A+n_B$ $=$ $\frac{(P_A+P_B)\;V}{RT}$ $=$ $\frac{P\;V}{RT}$ where: $n_A$ is the number of moles of $A$ in the gas phase $n_B$ is the number of moles of $B$ in the gas phase from which it results for the molar fractions $Y_A$ et $Y_B$ in the gas phase: $y_A=\frac{n_A}{n_A+n_B}=\frac{P_A}{P_A+P_B}=\frac{P_A}{P}=X_A\frac{P_oA}{P}$ $y_B=\frac{n_B}{n_A+n_B}=\frac{P_B}{P_A+P_B}=\frac{P_B}{P}=X_A\frac{P_oB}{P}$
The mole fractions in a gaseous phase in equilibrium with an ideal mixture of two liquids are: $Y_A=X_A\;\frac{P_{oA}}{P}$ $Y_B=X_B\;\frac{P_{oB}}{P}$ where: $X_A$ is the molar fraction of $A$ in the liquid phase $X_B$ is the molar fraction of $B$ in the liquid phase $P_{oA}$ is the saturation vapor pressure of $A$ $P_{oB} $ is the saturation vapor pressure of $B$ $P$ is the total pressure of the gas phase
Here are observed deviations from Raoult's Law.
The two vapour pressures decrease, because $A$ and $B$ want to stay together in the liquid:

The two vapour pressures increase, because $A$ and $B$ want to leave and escape from the liquid: