The converging lens

A converging lens is a biconvex glass that forms an inverted image of an object (like the dark room!).

Sketch

The lens is shown schematically. The point $A_1$ is the image of the point $A$

The image formation

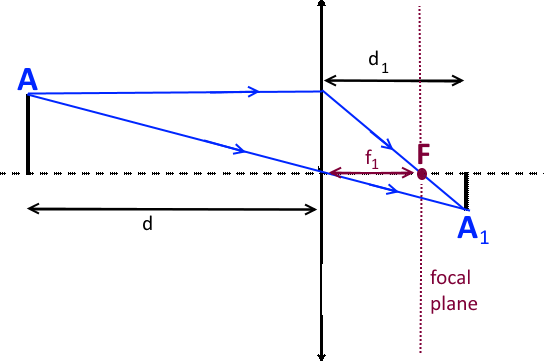
Each point $A$ of the object emits light rays in all directions It can be shown: - All rays from $A$ and passing through the lens converge to the same point $A_1$ - The ray passing through the optical center is not deflected. - The ray parallel to the optical axis intersects it at a point $F$ which is the focus of the lens. - The focal length $f_1$ is a characteristic of the lens in question. It does not depend on the position of point $A $, so it is the same for all points of the object!

The Law

There is a law linking the focal length $f_1$ to the distances $d$ and $d_1$ of object and image points to the vertical axis of the lens. It can be shown:

The object at infinity

For $d\rightarrow\infty$, we have: $\frac{1}{d}\rightarrow 0$ and so: $d_1\approx f_1$